题目内容
4.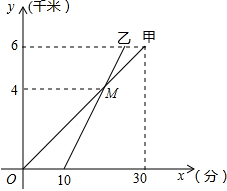 已知A、B两地的路程是6千米.甲骑自行车、乙骑摩托车,他们沿相同路线由A地到B地走完全程,甲、乙行驶过程中的路程随时间变化的函数关系的图象如图所示,根据图象解决下列问题:
已知A、B两地的路程是6千米.甲骑自行车、乙骑摩托车,他们沿相同路线由A地到B地走完全程,甲、乙行驶过程中的路程随时间变化的函数关系的图象如图所示,根据图象解决下列问题:(1)分别求出甲、乙两人行驶路程y(单位:千米)与时间x(单位:分)的函数关系式(不要求写出自变量的取值范围);
(2)求当x为何值时,两人相距1千米?
分析 (1)设y甲=k1x,将(30,6)代入,利用待定系数法求出甲行驶路程y与时间x的函数关系式;再求出M点坐标,设y乙=k2x+b,将点(10,0)和(20,4)代入,利用待定系数法求出乙行驶路程y与时间x的函数关系式;
(2)两人相距1千米时,分两种情况:①y甲-y乙=1;②y乙-y甲=1.分别列出方程,解方程即可.
解答  解:(1)设y甲=k1x,
解:(1)设y甲=k1x,
∵y甲=k1x的图象经过(30,6),
∴30k1=6,解得k1=$\frac{1}{5}$,
∴y甲=$\frac{1}{5}$x.
∵点M在y甲=$\frac{1}{5}$x的图象上,
∴当y=4时,即4=$\frac{1}{5}$x,
解得:x=20,
∴M(20,4).
设y乙=k2x+b,
由图象知y乙=k2x+b经过点(10,0)和(20,4),
则$\left\{\begin{array}{l}{0=10{k}_{2}+b}\\{4=20{k}_{2}+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=\frac{2}{5}}\\{b=-4}\end{array}\right.$,
∴y乙=$\frac{2}{5}$x-4;
(2)分两种情况:
①若y甲-y乙=1,则$\frac{1}{5}$x-($\frac{2}{5}$x-4)=1,解得x=15;
②若y乙-y甲=1,则($\frac{2}{5}$x-4)-$\frac{1}{5}$x=1,解得x=25.
综上所述,当x为15分或25分时,两人相距1千米.
点评 本题考查了一次函数的应用,用待定系数法求一次函数的解析式,借助函数图象表达题目中的信息,读懂图象是解题的关键.

练习册系列答案
相关题目
12.某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表:
(1)第一个月:用54000元购进A、B两种型号的手机,全部售完后获利9450元,求第一个月购进A、B两种型号手机的数量;
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
| 型 号 | A | B |
| 进 价 | 1800元/部 | 1500元/部 |
| 售 价 | 2070元/部 | 1800元/部 |
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.
如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=6.6m.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=6.6m.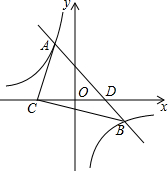 如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称.
如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称.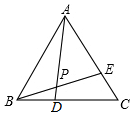 如图,△ABC是等边三角形,点D、E分别是BC、AC边上的两点,其中BD=CE,连接AD、BE交于点P
如图,△ABC是等边三角形,点D、E分别是BC、AC边上的两点,其中BD=CE,连接AD、BE交于点P 已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.
已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.