题目内容
6.已知(x+m)2=x2+nx+36,则n的值为( )| A. | ±6 | B. | ±12 | C. | ±18 | D. | ±72 |
分析 先将等式的左边根据完全平方公式展开,再根据等式的恒等原理就可以求出结论.
解答 解:∵(x+m)2=x2+2mx+m2,
∴x2+2mx+m2=x2+nx+36,
∴$\left\{\begin{array}{l}{2m=n}\\{{m}^{2}=36}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{m}_{1}=6}\\{{n}_{1}=12}\end{array}\right.$,$\left\{\begin{array}{l}{{m}_{2}=-6}\\{{n}_{2}═-12}\end{array}\right.$
故选:B.
点评 本题考查了完全平方公式的运用,等式的恒等原理的运用,熟练掌握完全平方公式的结构特征是关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
1. 如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )
如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )
如图,在?ABCD中,对角线AC、BD相交于点O,AC=10,BD=6,AD=4,则?ABCD的面积是( )| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24 | D. | 30 |
18.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表:
(1)如表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式;
(3)当所挂物体的质量为11.5kg时,求弹簧的长度.
| 所挂物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧的长度y(cm) | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(2)写出y与x之间的关系式;
(3)当所挂物体的质量为11.5kg时,求弹簧的长度.
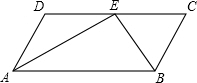 如图,平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.
如图,平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线. 已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.
已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长. 如图所示,由三角形ABC平移得到的三角形有5个.
如图所示,由三角形ABC平移得到的三角形有5个.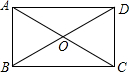 如图,在矩形ABCD中,AC,BD相交于点O,根据矩形的性质,AO=OB=OC=0D=$\frac{1}{2}$AC=$\frac{1}{2}$BD,由此我们得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半.
如图,在矩形ABCD中,AC,BD相交于点O,根据矩形的性质,AO=OB=OC=0D=$\frac{1}{2}$AC=$\frac{1}{2}$BD,由此我们得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半.