题目内容
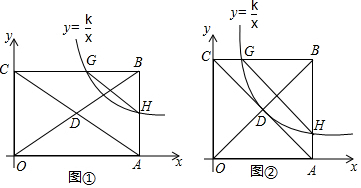
20.如图,①,A(4,0),C(0,n)分别是x和y轴上的点,n>0,以OA,OC为边在第一象限内作矩形OABC,对角线OB,AC,交于点D双曲线y=$\frac{k}{x}$(x>0,k>0)交边BC于G,交边AB于H.(1)设直线AC的函数关系式为y=qx+p,请用含n的代数式表示q和p;
(2)求证:AB•BG=BC•BH;
(3)如图②,若上述双曲线经过点D,判断点D是否是双曲线与直线AC唯一的交点,请说明理由.
分析 (1)把A、C坐标代入可得到关于n与p、q的关系式,可求得答案;
(2)可用n和k分别表示出G、H的坐标,则可证得$\frac{BG}{BC}$=$\frac{BH}{BA}$,可证得结论;
(3)可用n表示出D点坐标,从而可用n表示出k,则可表示出反比例函数的解析式,联立直线AC与反比例函数解析式,可证得结论.
解答 (1)解:∵A(4,0),C(0,n),
∴$\left\{\begin{array}{l}{4q+p=0}\\{p=n}\end{array}\right.$,
∴q=-$\frac{n}{4}$,p=n;
(2)证明:
∵四边形OABC为矩形,
∴BC=OA=4,AB=OC=n,
∴G($\frac{k}{n}$,n),H(4,$\frac{k}{4}$),
∴BG=4-$\frac{k}{n}$,BH=n-$\frac{k}{4}$,
∴$\frac{BG}{BH}$=$\frac{4-\frac{k}{n}}{n-\frac{k}{4}}$=$\frac{4}{n}$=$\frac{BC}{BA}$,
∴AB•BG=BC•BH;
(3)解:点D是双曲线与直线AC唯一的交点,
理由如下:
∵A(4,0),C(0,n),
∴D(2,$\frac{n}{2}$),
∵双曲线经过点D,
∴k=2×$\frac{n}{2}$=n,
∴双曲线解析式为y=$\frac{n}{x}$,
由(1)可知直线AC解析式为y=-$\frac{n}{4}$x+n,
联立直线与双曲线解析式可得$\left\{\begin{array}{l}{y=-\frac{n}{4}x+n}\\{y=\frac{n}{x}}\end{array}\right.$,消去y整理可得x2-4x+4=0,
∵方程x2-4x+4=0有两个相等的实数根,
∴直线AC与双曲线有唯一一个交点D.
点评 本题为反比例函数的综合应用,涉及待定系数法、矩形的性质、反比例函数图象上点的坐标特征、函数图象的交点等知识.在(1)中注意待定系数法的应用,在(2)中表示出B、G的坐标是解题的关键,在(3)中用n表示出直线AC与双曲线的解析式是解题的关键.本题考查知识点较多,综合性较强,难度适中.

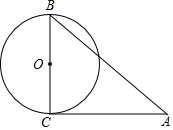 如图,⊙O半径为4,BC是直径,AC是⊙O的切线,且AC=6,那么AB=( )
如图,⊙O半径为4,BC是直径,AC是⊙O的切线,且AC=6,那么AB=( )| A. | 4 | B. | 6 | C. | 10 | D. | 12 |
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
| A. | 1 | B. | -1 | C. | -4 | D. | 4 |