题目内容
6.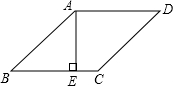 如图,在菱形ABCD中,AE⊥BC于E,AE=2cm,sinB=$\frac{1}{3}$,求:
如图,在菱形ABCD中,AE⊥BC于E,AE=2cm,sinB=$\frac{1}{3}$,求:(1)菱形的周长;
(2)求sin∠BAE.
分析 (1)由菱形的性质得出AB=BC=CD=AD,由三角函数求出AB,即可得出菱形的周长;
(2)由勾股定理求出BE,即可求出sin∠BAE.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵AE⊥BC,
∴∠AEB=90°,
∴sinB=$\frac{AE}{AB}$,
∴AB=$\frac{AE}{sinB}$=$\frac{2}{\frac{1}{3}}$=6(cm),
∴菱形的周长=4AB=4×6=24(cm);
(2)由勾股定理得:BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
∴sin∠BAE=$\frac{BE}{AB}=\frac{4\sqrt{2}}{6}$=$\frac{2\sqrt{2}}{3}$.
点评 本题考查了菱形的性质、菱形周长的计算、勾股定理、三角函数;熟练掌握勾股定理和三角函数是解决问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
18.点(-5,y1)和点(-2,y2)都在一次函数y=-2x的图象上,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法确定 |
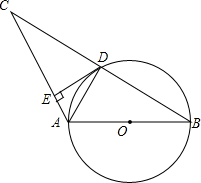 如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.
如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.