题目内容
14.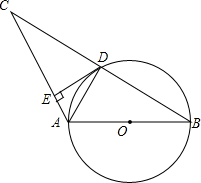 如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.
如图,AB是⊙0的直径,⊙0经过△ABC的边BC的中点D,DE⊥AC,垂足为E.(1)求证:DE是⊙0的切线;
(2)若AE=1,AB=4,求AD的长.
分析 (1)连接OD.根据三角形的中位线定理,得OD∥AC,结合DE⊥AC,即可证明OD⊥DE,从而证明DE是⊙O的切线.
(2)根据直径所对的圆周角是直角,得AD⊥BC,结合BD=CD即可证明AB=AC=4,求得CE=3,然后根据射影定理求得DE2,再根据勾股定理即可求得AD.
解答 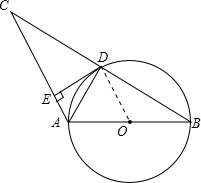 (1)证明:连接OD.
(1)证明:连接OD.
∵OA=OB,BD=CD,
∴OD∥AC.
又DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)解:∵AB是⊙O的直径,
∴AD⊥BC,
又BD=CD,
∴AB=AC=4,
∵AE=1,
∴CE=4-1=3,
在RT△ADC中,DE⊥AC,
∴DE2=AE•CE=1×3=3,
∴AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=2.
点评 考查了切线的判定,此题综合运用了圆周角定理、线段垂直平分线定理、三角形的中位线定理、勾股定理、平行线的性质以及切线的判定定理.

练习册系列答案
相关题目
9.若xy=xz成立,则下列式子未必成立的是( )
| A. | y=z | B. | x(y+1)=x(z+1) | C. | xy2=xyz | D. | x(y-1)=x(z-1) |
19.小明在解方程3x-(x-2a)=4去括号时,忘记将括号中的第二项变号,求得方程的解为x=-2,那么方程正确的解为( )
| A. | x=2 | B. | x=4 | C. | x=6 | D. | x=8 |
 如图,D,E,F分别是△ABC边上一点,且AD=AF,BD=BE.
如图,D,E,F分别是△ABC边上一点,且AD=AF,BD=BE.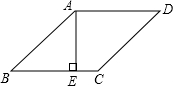 如图,在菱形ABCD中,AE⊥BC于E,AE=2cm,sinB=$\frac{1}{3}$,求:
如图,在菱形ABCD中,AE⊥BC于E,AE=2cm,sinB=$\frac{1}{3}$,求: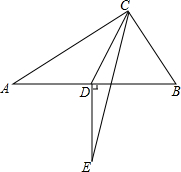 已知,如图:在△ABC中,∠ACB=90°,AB的垂直平分线DE,交∠ACB的平分线于点E,交AB于点D.
已知,如图:在△ABC中,∠ACB=90°,AB的垂直平分线DE,交∠ACB的平分线于点E,交AB于点D.