题目内容
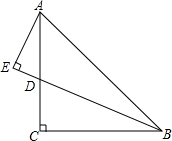 如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=
如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=| 1 |
| 2 |
考点:全等三角形的判定与性质
专题:证明题
分析:延长AE,BC交于点F,易证∠EAD=∠CBD,即可求证△ACF≌△BCD,可得AF=BD,易证△ABE≌△FBE,可得AE=EF,即可解题.
解答:证明:延长AE,BC交于点F,
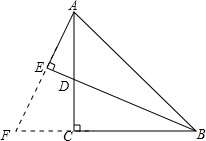
∵∠EAD+∠ADE=90°,∠BDC+∠CBD=90°,∠ADE=∠BDC
∴∠EAD=∠CBD,
∵在△ACF和△BCD中,
,
∴△ACF≌△BCD,(ASA)
∴AF=BD,
∵在△ABE和△FBE中,
,
∴△ABE≌△FBE,(ASA)
∴AE=EF,即AE=
AF,
∴AE=
BD.

∵∠EAD+∠ADE=90°,∠BDC+∠CBD=90°,∠ADE=∠BDC
∴∠EAD=∠CBD,
∵在△ACF和△BCD中,
|
∴△ACF≌△BCD,(ASA)
∴AF=BD,
∵在△ABE和△FBE中,
|
∴△ABE≌△FBE,(ASA)
∴AE=EF,即AE=
| 1 |
| 2 |
∴AE=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACF≌△BCD和△ABE≌△FBE是解题的关键.

练习册系列答案
相关题目
 如图,AB,BC,CD都与半圆相切,A、D是切点.其中AB=4,CD=9,BC=13,则半圆的半径是( )
如图,AB,BC,CD都与半圆相切,A、D是切点.其中AB=4,CD=9,BC=13,则半圆的半径是( )| A、12 | B、10 | C、8 | D、6 |
 已知,AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,求△PCD的面积的最小值是多少?
已知,AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,求△PCD的面积的最小值是多少? 如图所示,等边△ABC中,D是三角形内一点,DA=DB,BE=AB,∠CBD=∠EBD,求∠E的度数.
如图所示,等边△ABC中,D是三角形内一点,DA=DB,BE=AB,∠CBD=∠EBD,求∠E的度数.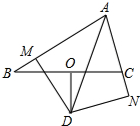 如图,△ABC中,O是BC的中点,D是∠BAC平分线上一点,且DO⊥BC,过点D分别作DM⊥AB于M,DN⊥AC于N.求证:
如图,△ABC中,O是BC的中点,D是∠BAC平分线上一点,且DO⊥BC,过点D分别作DM⊥AB于M,DN⊥AC于N.求证: