题目内容
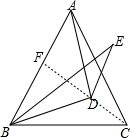
 如图所示,等边△ABC中,D是三角形内一点,DA=DB,BE=AB,∠CBD=∠EBD,求∠E的度数.
如图所示,等边△ABC中,D是三角形内一点,DA=DB,BE=AB,∠CBD=∠EBD,求∠E的度数.考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:连接CD延长至E,易证△BCD≌△BED,可得∠E=∠BCD,根据DA=DB,CA=CB可得CD是AB的垂直平分线,根据等边三角形三线合一的性质即可求得∠BCD的值,即可解题.
解答:解:连接CD延长至E,
∵AB=BC,AB=BE,
∴BE=BC,
∵在△BCD和△BED中,
,
∴△BCD≌△BED,(SAS)
∴∠E=∠BCD,
∵DA=DB,CA=CB,
∴CD是AB的垂直平分线,
∴CF是等边△ABC中∠ACB的平分线,
∴∠E=∠BCD=30°.

∵AB=BC,AB=BE,
∴BE=BC,
∵在△BCD和△BED中,
|
∴△BCD≌△BED,(SAS)
∴∠E=∠BCD,
∵DA=DB,CA=CB,
∴CD是AB的垂直平分线,
∴CF是等边△ABC中∠ACB的平分线,
∴∠E=∠BCD=30°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,考查了等边三角形三线合一的性质,考查了垂直平分线的判定,本题中求证△BCD≌△BED是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求:
如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求: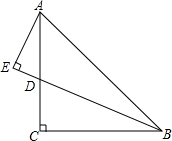 如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=
如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=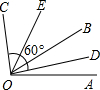 如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数.
如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数. 如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D.
如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D.