题目内容
若一个二次函数图象经过点A(-1,5)、B(3,5)、C(-2,-6),求这个函数的表达式及它的图象的对称轴、顶点坐标.
考点:待定系数法求二次函数解析式
专题:计算题
分析:设抛物线解析式为y=ax2+bx+c,把A,B,C坐标代入求出a,b,c的值,确定出解析式,即可求出对称轴以及顶点坐标.
解答:解:设抛物线解析式为y=ax2+bx+c,
把A(-1,5),B(3,5),C(-2,-6)代入得:
,
解得:a=-
,b=
,c=
,
则抛物线解析式为y=-
x2+
x+
,对称轴为直线x=1,顶点坐标为(1,
).
把A(-1,5),B(3,5),C(-2,-6)代入得:
|
解得:a=-
| 11 |
| 5 |
| 22 |
| 5 |
| 58 |
| 5 |
则抛物线解析式为y=-
| 11 |
| 5 |
| 22 |
| 5 |
| 58 |
| 5 |
| 69 |
| 5 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
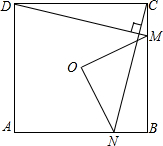 如图,O是正方形ABCD的中心,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM,交AB于点N,连接OM、ON.求证:
如图,O是正方形ABCD的中心,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM,交AB于点N,连接OM、ON.求证: 现有一张缺损一角的矩形纸片,如图,在矩形ABCD中,AB=8cm,BC=10cm,AE=3cm,AF=4cm,要从中裁出一张矩形纸片,则裁出的面积最大的矩形纸片的对角线长为
现有一张缺损一角的矩形纸片,如图,在矩形ABCD中,AB=8cm,BC=10cm,AE=3cm,AF=4cm,要从中裁出一张矩形纸片,则裁出的面积最大的矩形纸片的对角线长为
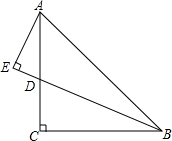 如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=
如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=