题目内容
一个运动员推铅球,铅球刚出手时铅球距地面
m,当铅球运动员水平距离4m时达到最高点3.2m.假设铅球行进的轨迹是抛物线,你能算出这个与动员的成绩吗?
| 16 |
| 9 |
考点:二次函数的应用
专题:
分析:设铅球行进的轨迹的抛物线的解析式为y=a(x-4)2+3.2,由待定系数法求出二次函数的解析式,在当y=0时求出x的值即可.
解答:解:设铅球行进的轨迹的抛物线的解析式为y=a(x-4)2+3.2,由题意,得
=a(0-4)2+3.2,
解得:a=-
,
∴y=-
(x-4)2+3.2.
当y=0时,
-
(x-4)2+3.2=0,
解得:x1=10,x2=-2(舍去).
答:这个与动员的成绩是10米.
| 16 |
| 9 |
解得:a=-
| 4 |
| 45 |
∴y=-
| 4 |
| 45 |
当y=0时,
-
| 4 |
| 45 |
解得:x1=10,x2=-2(舍去).
答:这个与动员的成绩是10米.
点评:本题考查运用待定系数法求二次函数的解析式的运用,由函数值求自变量的值的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求:
如图,AB为⊙O的直径,PF切⊙O于A,△ABC是⊙O的内接三角形,AC=8,过C作CF与AB、PA、⊙O分别交于E、D、F,CE:ED=6:5,AE:EB=2:3,求: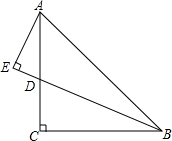 如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=
如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上的一点,且AE⊥BD的延长线交于E,又BD平分∠ABC,求证:AE=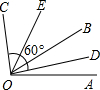 如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数.
如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数. 某自然景区有一块长12米,宽8米的矩形花圃(如图所示),喷水无安装在矩对角线的交点P上,现计算从P点引3条射线,把花圃分成面积相等的三部分,分别种植三种不同的花,如果不考虑分不分的间隙.
某自然景区有一块长12米,宽8米的矩形花圃(如图所示),喷水无安装在矩对角线的交点P上,现计算从P点引3条射线,把花圃分成面积相等的三部分,分别种植三种不同的花,如果不考虑分不分的间隙. 如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D.
如图,AB•AE=AC•AD,∠1=∠2,求证:∠B=∠D.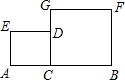 如图,已知线段AB=6,在线段AB上有一点C(不同于A、B),分别以AC、BC为边在AB同侧作正方形ACDE、CBFG,设AC=x.
如图,已知线段AB=6,在线段AB上有一点C(不同于A、B),分别以AC、BC为边在AB同侧作正方形ACDE、CBFG,设AC=x.