题目内容
12.若a,b,c是△ABC的三边,化简:$\sqrt{(a+b+c)^{2}}$-$\sqrt{(a-b-c)^{2}}$+$\sqrt{(b-c-a)^{2}}$-$\sqrt{(c-a-b)^{2}}$.分析 利用三角形三边关系得出各项符号,再利用二次根式的性质化简求出即可.
解答 解:∵a,b,c是△ABC的三边,
∴a-b-c<0,b-c-a<0,c-a-b<0,
∴$\sqrt{(a+b+c)^{2}}$-$\sqrt{(a-b-c)^{2}}$+$\sqrt{(b-c-a)^{2}}$-$\sqrt{(c-a-b)^{2}}$
=a+b+c+a-b-c-(b-c-a)+c-a-b
=2a-2b+2c.
点评 此题主要考查了二次根式的性质与化简以及三角形三边关系,正确开平方是解题关键.

练习册系列答案
相关题目
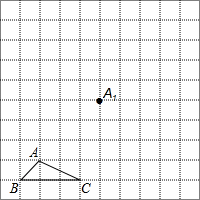 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).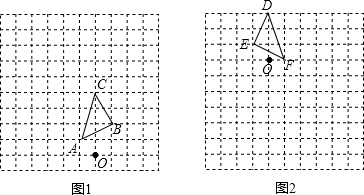
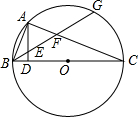 如图,BC是⊙O的直径,G为弧$\widehat{AC}$的中点,AD⊥BC于D,求证:AE=AF.
如图,BC是⊙O的直径,G为弧$\widehat{AC}$的中点,AD⊥BC于D,求证:AE=AF.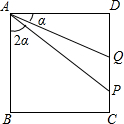 如图,在正方形ABCD中,AB=8,Q是CD的中点,设∠DAQ=α,在CD上取一点P,使∠BAP=2α,求CP的长度.
如图,在正方形ABCD中,AB=8,Q是CD的中点,设∠DAQ=α,在CD上取一点P,使∠BAP=2α,求CP的长度.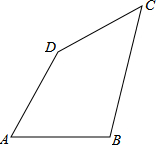 如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积.
如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积. 如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.