题目内容
18.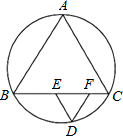 如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
分析 先由弧的比即可得出弧所对的圆周角的比,再用三角形的内角和即可求出∠BAC,∠ABC,∠ACB,进而用平行线的性质得出∠DEF,∠DFE,最后用三角形的内角和定理即可得出结论.
解答 解:∵$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,
∴∠ACB:∠BAC:∠ABC=12:13:11,
设∠ACB=12x,∠BAC=13x,∠ABC=11x,
∵∠ACB+∠BAC+∠ABC=180°,
∴12x+13x+11x=180°,
∴x=5°,
∴∠ACB=12x=60°,∠BAC=13x=65°,∠ABC=11x=55°,
∵DE∥AC,
∴∠DEF=∠ACB=60°,
∵DF∥AB,
∴∠DFE=∠ABC=55°,
∴∠EDF=180°-∠DEF-∠DFE=60°,
选B.
点评 此题主要同圆中,弧的比等于弧所对圆周角的比,三角形的内角和公式,平行线的性质,解本题的关键是求出∠ABC,∠ACB,∠BAC的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若a与b互为相反数,则|a+b-2|等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
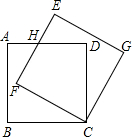 如图,边长为10的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为$\frac{10\sqrt{3}}{3}$.
如图,边长为10的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为$\frac{10\sqrt{3}}{3}$. 如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD.
如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD.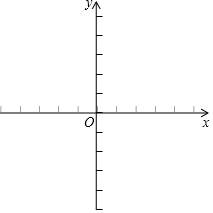 已知.
已知. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,像这样的三角形叫做格点三角形.若下列每个小正方形的边长均为1,试在下面5×5的方格纸上按要求解决下列问题:
如图,△ABC的顶点A、B、C都在小正方形的顶点上,像这样的三角形叫做格点三角形.若下列每个小正方形的边长均为1,试在下面5×5的方格纸上按要求解决下列问题: