题目内容
6.用五种不同的颜色,把△ABC的3个顶点染上其中的一种颜色.(1)如果要求三条边的两端点都有不同的颜色,则有多少种不同的染色方法?
(2)如果只要求A、B异色,则有多少种不同的染色法?
分析 (1)先确定出一个顶点A的颜色,再确定出点B的颜色的选用颜色的种数,最后确定出点C选用颜色的种数,即可得出结论;
(2)先确定出点A的颜色,再确定出点B的颜色,最后确定出点C的颜色选用方法,即可得出结论.
解答 解:(1)∵三条边的两端点都有不同的颜色,
∴顶点A,B,C上的颜色都不相同,
∴有五种不同的颜色,
∴点A处有5种染色方法,
点B在点A用过剩余的4种颜色中,选用一种染色,有4种染色方法,
点C在剩余的三种颜色中,任选一种,有3种染色方法,
所以一共有5×4×3=60种不同的染色方法;
(2)∵A、B异色,
∴点A在5中颜色种选用一种,
则点B在剩余的4种颜色中,选用一种染色,有四种方法,
点C五种颜色中,任选一种,有5种染法,
所以,一共有5×4×5=100种不同的染色方法.
点评 此题是染色问题,主要考查了学生的分析问题和解决问题,解本题的关键是确定出每个顶点颜色的种数.

练习册系列答案
相关题目
10. 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
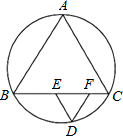 如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( ) 平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=$\frac{k}{x}$的图象经过点C.
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=$\frac{k}{x}$的图象经过点C.