题目内容
3. 如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD.
如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD.
分析 由题可知,AD和BE平行,得出△EBC∽△ADC,根据对应边成比例列式求解即可.
解答 解:∵BE∥AD,
∴△EBC∽△ADC,
∴$\frac{EB}{AD}$=$\frac{BC}{DC}$=$\frac{50}{80}$=$\frac{5}{8}$,
∴AD=$\frac{8}{5}$BE=$\frac{8}{5}$×20=32(米);
答:甲楼高AD为32米.
点评 本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.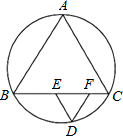 如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
 如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
13.数轴上的一点M对应的数为-1,点N表示的数比点M表示的数大3,则点N表示的数为( )

| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
