题目内容
10.若x≠y,则x4+y4>x3y+xy3(填“>”或“<”)分析 首先作差,利用因式分解得出:(x4+y4)-(x3y+xy3)>0即可得出结论.
解答 解:(x4+y4)-(x3y+xy3)
=x4+y4-x3y-xy3)
=x3(x-y)-y3(x-y)
=(x-y)(x3-y3)
=(x-y)2(x2+xy+y2),
=(x-y)2[(x+$\frac{1}{2}$y)2+$\frac{3}{4}$y2]
∵x≠y,(x-y)2>0,[(x+$\frac{1}{2}$y)2+$\frac{3}{4}$y2]>0,
∴(x-y)2[(x+$\frac{1}{2}$y)2+$\frac{3}{4}$y2]>0,
∴x4+y4>x3y+xy3.
故答案为:>.
点评 此题考查因式分解的实际运用,比较法是证明不等式的一种最重要最基本的方法.作差法的三个步骤:作差--变形--判断符号(与零的大小)--结论.

练习册系列答案
相关题目
18.某村准备在坡度(坡面的铅直高度与水平宽度之比)为$\frac{1}{3}$的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离为( )米.
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$$\sqrt{10}$ | D. | $\sqrt{10}$ |
2.某班统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如下表,则这10名同学在一周内累计时间的众数是( )
| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
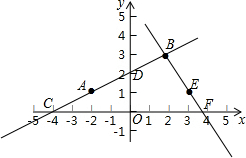 连接AB,直线AB与x轴交于点C,与y轴交于点D,平面内有一点E(3,1),直线BE与x轴交于点F.直线AB的解析式记作y1=kx+b,直线BE解析式记作y2=mx+t.求:
连接AB,直线AB与x轴交于点C,与y轴交于点D,平面内有一点E(3,1),直线BE与x轴交于点F.直线AB的解析式记作y1=kx+b,直线BE解析式记作y2=mx+t.求:



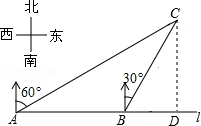 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km.
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km.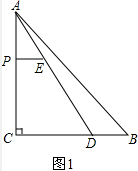 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,D是BC边上一点,CD=3cm,点P为边AC上一动点(点P与A、C不重合),过点P作PE∥BC,交AD于点E,点P以1cm/s的速度从A到C匀速运动.设点P的运动时间为t(s),DE的长为y(cm),求y关于t的函数关系式,并写出t的取值范围.