题目内容
19．先化简，再求值：（a+$\frac{1}{a+2}$）÷（a-2+$\frac{3}{a+2}$），请从-1，0，1中选取一个作为a的值代入求值．分析 首先对括号内的分式通分相加，然后转化为乘法计算，即可化简，然后选取一个能使分式有意义的x的值代入求解．
解答 解：原式=$\frac{{a}^{2}+2a+1}{a+2}$÷$\frac{{a}^{2}-1}{a+2}$
=$\frac{（a+1）^{2}}{a+2}$•$\frac{a+2}{（a+1）（a-1）}$
=$\frac{a+1}{a-1}$，
∵当a取-1和1时，原式无意义．
∴把a=0代入．原式=-1．
点评 本题考查了分式的化简求值，正确对分式进行通分、约分是关键．
练习册系列答案
相关题目
如图为一组有规律的图案，则第n个图案中“●”和“△”的个数之和为（n+1）2+4n．（用含n的代数式表示）
4．-3+（-5）×（-1）的结果是（ ）
| A． | -2 | B． | -1 | C． | 2 | D． | 1 |
11．
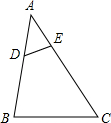如图，在△ABC中，点D、E分别在AB、AC上，∠AED=∠B，如果AE=2，△ADE的面积为4，四边形BCED的面积为21，那么AB的长为（ ）
如图，在△ABC中，点D、E分别在AB、AC上，∠AED=∠B，如果AE=2，△ADE的面积为4，四边形BCED的面积为21，那么AB的长为（ ）| A． | 5 | B． | 12.5 | C． | 25 | D． | $\sqrt{21}$ |
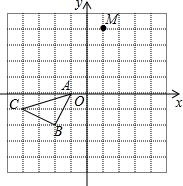如图，在边长为1个单位长度的小正方形组成的格点图中，点A、B、C都是格点．