题目内容
15.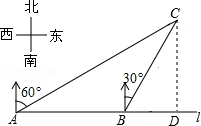 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km.
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏东30°的方向,测船C离海岸线l的距离(即CD的长为)$\sqrt{3}$km.
分析 首先由题意可证得:△ACB是等腰三角形,即可求得BC的长,然后由在Rt△CBD中,CD=BC•sin60°,求得答案.
解答 解:根据题意得:∠CAD=90°-60°=30°,∠CBD=90°-30°=60°,
∴∠ACB=∠CBD-∠CAD=30°,
∴∠CAB=∠ACB,
∴BC=AB=2km,
在Rt△CBD中,CD=BC•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(km).
故答案为:$\sqrt{3}$.
点评 此题考查了方向角问题.注意证得△ABC是等腰三角形是解此题的关键.

练习册系列答案
相关题目
5.算式:(-4)-2的计算结果是( )
| A. | -16 | B. | $\frac{1}{16}$ | C. | 16 | D. | $-\frac{1}{16}$ |
6. 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
 如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )
如图,OC平分平角∠AOB,∠AOD=∠BOE=20°,图中互余的角共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
3.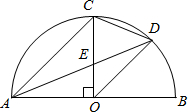 如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
 如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )
如图,AB是半圆O(的)直径,半径OC⊥AB,连线AC,∠CAB的平分线AD分别交OC于点E,交$\widehat{BC}$于点D,连接CD、OD.以下结论错误的是( )| A. | AC∥OD | B. | CD2=CE•CO | C. | S△AEC=2S△DOE | D. | AC=2CD |
4.-3+(-5)×(-1)的结果是( )
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
 如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)
如图为一组有规律的图案,则第n个图案中“●”和“△”的个数之和为(n+1)2+4n.(用含n的代数式表示)