题目内容
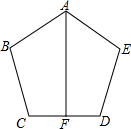 如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点. (1)求证:AF⊥CD.
(2)连接BE,AC,AD,标出相应的交点,你能从图中发现什么新的结论?请写出3个,并相互交流.
考点:全等三角形的判定与性质
专题:
分析:(1)如图,连接AC、AD.通过全等三角形的判定定理SAS证得△ABC≌△AED,则对应边相等:AC=AD;然后根据等腰三角形“三线合一”的性质证得结论;
(2)如图,连接BE,设BE与AC、AF、AD的交点分别是E、G、F.根据(1)的证明过程知△ABC与△AED关于直线AF对称,根据对称的性质,同(1)证得相关全等三角形,可以推知BE=EF,AE=AF,EG=FG.
(2)如图,连接BE,设BE与AC、AF、AD的交点分别是E、G、F.根据(1)的证明过程知△ABC与△AED关于直线AF对称,根据对称的性质,同(1)证得相关全等三角形,可以推知BE=EF,AE=AF,EG=FG.
解答: (1)证明:如图,连接AC、AD.
(1)证明:如图,连接AC、AD.
在△ABC与△AED中,
,
∴△ABC≌△AED(SAS),
∴AC=AD.
又∵F是边CD的中点,
∴AF⊥CD;
(2)解:如图,连接BE,设BE与AC、AF、AD的交点分别是E、G、F.BE=EF,AE=AF,EG=FG.理由如下:
由(1)知,△ABC≌△AED,△ACD的等腰三角形,
∴△ABC与△AED关于直线AF对称,
∴△ABE≌△AEF,△AEG≌△AFG,
∴BE=EF,AE=AF,EG=FG.
 (1)证明:如图,连接AC、AD.
(1)证明:如图,连接AC、AD.在△ABC与△AED中,
|
∴△ABC≌△AED(SAS),
∴AC=AD.
又∵F是边CD的中点,
∴AF⊥CD;
(2)解:如图,连接BE,设BE与AC、AF、AD的交点分别是E、G、F.BE=EF,AE=AF,EG=FG.理由如下:
由(1)知,△ABC≌△AED,△ACD的等腰三角形,
∴△ABC与△AED关于直线AF对称,
∴△ABE≌△AEF,△AEG≌△AFG,
∴BE=EF,AE=AF,EG=FG.
点评:本题考查了全等三角形判定与性质.(2)题属于开放题,答案不唯一,根据全等三角形的判定与性质还可以得到∠EAG=∠FAG、∠BAF=∠EAG等结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于D、E,AB=1,则cos∠C等于( )
如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于D、E,AB=1,则cos∠C等于( )| A、DE | B、AC | C、CE | D、BC |
 如图,已知抛物线L1:y1=
如图,已知抛物线L1:y1=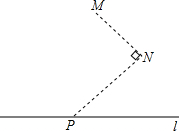 如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.
如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.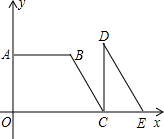 四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-
四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-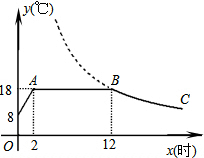 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=