题目内容
 如图,已知抛物线L1:y1=
如图,已知抛物线L1:y1=| 3 |
| 4 |
(1)求抛物线L2的解析式;
(2)判断△ABC的形状,并说明理由;
(3)点P为抛物线L2上的动点,过点P作PD⊥x轴,与抛物线L1交于点D,是否存在PD=2OC?若存在,求出点P的坐标;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)由于二次函数的二次项系数表示的是抛物线的开口大小和开口方向,在平移过程中,抛物线的形状没有发生变化,所以二次项系数仍为
,已知了平移后的抛物线经过x轴上的A、B两点,可由待定系数法求出平移后的抛物线解析式;
(2)由坐标轴上点的特征可得C(0,-3),根据两点间的距离公式得到AB,BC,AC的值,再根据等腰三角形的判定即可求解;
(3)可设P(a,
a2-
a-3),D(a,
a2),根据PD=2OC,列出方程即可求解.
| 3 |
| 4 |
(2)由坐标轴上点的特征可得C(0,-3),根据两点间的距离公式得到AB,BC,AC的值,再根据等腰三角形的判定即可求解;
(3)可设P(a,
| 3 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
解答:解:(1)设抛物线L2的解析式为y=
x2+bx+c,经过点A(-1,0),B(4,0),根据题意,得
,
解得
∴抛物线L2的解析式为y=
x2-
x-3.
(2)△ABC的形状是等腰三角形.
理由:根据题意,得C(0,-3),
∵AB=4-(-1)=5,BC=
=5,AC=
=
,
∴△ABC的形状是等腰三角形.
(3)存在PD=2OC.
设P(a,
a2-
a-3),D(a,
a2),
根据题意,得PD=|
a2-
a-3-
a2|=|
a+3|,OC=3,
当|
a+3|=6时,解得a1=
,a2=-4.
∴P1(
,
),P2(-4,18).
| 3 |
| 4 |
|
解得
|
∴抛物线L2的解析式为y=
| 3 |
| 4 |
| 9 |
| 4 |
(2)△ABC的形状是等腰三角形.
理由:根据题意,得C(0,-3),
∵AB=4-(-1)=5,BC=
| 42+32 |
| 12+32 |
| 10 |
∴△ABC的形状是等腰三角形.
(3)存在PD=2OC.
设P(a,
| 3 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
根据题意,得PD=|
| 3 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
当|
| 9 |
| 4 |
| 4 |
| 3 |
∴P1(
| 4 |
| 3 |
| 14 |
| 3 |
点评:此题考查了二次函数综合题,涉及了二次函数图象的平移、待定系数法求函数解析式、等腰三角形的判定以及两点间的距离等知识,综合性较强,难度中等.

练习册系列答案
相关题目
 实数a在数轴上的位置如图:化简:|a-1|+
实数a在数轴上的位置如图:化简:|a-1|+| (a-2)2 |
| A、1 | B、3 |
| C、2a-3 | D、无法确定 |
 如图,在△ABC中,已知∠C=90°,AC=8,BC=6,D是AC中点,过点D作DE⊥AB于E,求DE的长.
如图,在△ABC中,已知∠C=90°,AC=8,BC=6,D是AC中点,过点D作DE⊥AB于E,求DE的长. 如图,每个小正方形的边长都是1.
如图,每个小正方形的边长都是1.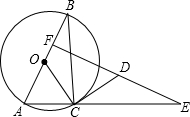 如图,圆O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是圆O的切线,ED⊥AB于F,
如图,圆O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是圆O的切线,ED⊥AB于F,
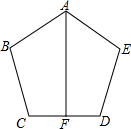 如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点.