题目内容
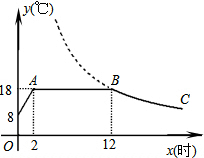 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=| k |
| x |
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
(4)一天24小时大棚内温度超过12℃的时间有多少小时?
考点:反比例函数的应用,一次函数的应用
专题:
分析:(1)根据图象直接得出大棚温度18℃的时间为12-2=10(小时);
(2)利用待定系数法求反比例函数解析式即可;
(3)将x=16代入函数解析式求出y的值即可;
(4)分别利用x的取值范围求出两函数解析式,进而得出y=12时,得出x的值即可.
(2)利用待定系数法求反比例函数解析式即可;
(3)将x=16代入函数解析式求出y的值即可;
(4)分别利用x的取值范围求出两函数解析式,进而得出y=12时,得出x的值即可.
解答:解:(1)恒温系统在这天保持大棚温度18℃的时间为:12-2=10(小时).
(2)∵点B(12,18)在双曲线y=
上,
∴18=
,
∴解得:k=216.
(3)当x=16时,y=
=13.5,
所以当x=16时,大棚内的温度约为13.5℃.
(4)当0≤x≤2时,直线解析式为:y=ax+b,
故
,
解得:
,
∴解析式为:y=5x+8,
则12=5x+8,
解得:x=0.8,
当y=12,则
=12,
解得:x=18,
∴一天24小时大棚内温度超过12℃的时间有:18-0.8=17.2(小时).
(2)∵点B(12,18)在双曲线y=
| k |
| x |
∴18=
| k |
| 12 |
∴解得:k=216.
(3)当x=16时,y=
| 216 |
| 16 |
所以当x=16时,大棚内的温度约为13.5℃.
(4)当0≤x≤2时,直线解析式为:y=ax+b,
故
|
解得:
|
∴解析式为:y=5x+8,
则12=5x+8,
解得:x=0.8,
当y=12,则
| 216 |
| x |
解得:x=18,
∴一天24小时大棚内温度超过12℃的时间有:18-0.8=17.2(小时).
点评:此题主要考查了反比例函数的应用以及待定系数法求一次函数解析式等知识,求出反比例函数解析式是解题关键.

练习册系列答案
相关题目
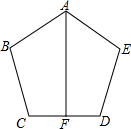 如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点.  如图,△ABC是等边三角形,M点在△ABC外部,N点在△ABC内部,若将△AMB绕点B顺时针旋转可得到△CNB,则∠MBN的度数为
如图,△ABC是等边三角形,M点在△ABC外部,N点在△ABC内部,若将△AMB绕点B顺时针旋转可得到△CNB,则∠MBN的度数为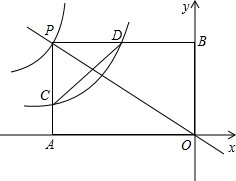 如图,经过原点的直线交双曲线y=-
如图,经过原点的直线交双曲线y=-