Question

17．九年级七班“数学兴趣小组”对函数的对称变换进行探究，以下是探究发现运用过程，请补充完整．
（1）操作发现，在作函数y=|x|的图象时，采用了分段函数的办法，该函数转化为y=$\left\{\begin{array}{l}{x}&{x≥0}\\{-x}&{x＜0}\end{array}\right.$，请在如图1所示的平面直角坐标系中作出函数的图象；
（2）类比探究
作函数y=|x-1|的图象，可以转化为分段函数$y=\left\{\begin{array}{l}{x-1（x≥1）}\\{-x+1（x＜1）}\end{array}\right.$，然后分别作出两段函数的图象．聪明的小昕，利用坐标平面上的轴对称知识，把函数y=x-1在x轴下面部分，沿x轴进行翻折，与x轴上及上面部分组成了函数y=|x-1|的图象，如图2左图所示；
（3）拓展提高
如图2右图是函数y=x²-2x-3的图象，请在原坐标系作函数y=|x²-2x-3|的图象；
（4）实际运用
1）函数y=|x²-2x-3|的图象与x轴有2个交点，对应方程|x²-2x-3|=0有2个实根；
2）函数y=|x²-2x-3|的图象与直线y=5有2个交点，对应方程|x²-2x-3|=5有2个实根；
3）函数y=|x²-2x-3|的图象与直线y=4有3个交点，对应方程|x²-2x-3|=4有3个实根；
4）关于x的方程|x²-2x-3|=a有4个实根时，a的取值范围是0＜a＜4．

Answer 1

分析 （1）利用描点法画y=|x|的图象；
（2）根据绝对值的意义，利用分类讨论的思想写出分段函数；
（3）与（2）画函数图象的方法一样，把函数y=x²-2x-3的图象在x轴下面部分，沿x轴进行翻折可得到函数y=|x²-2x-3|的图象；
（4）利用画函数图象，通过确定y=|x²-2x-3|的图象与直线y=a的交点个数解决问题．

解答 解：（1）操作发现
如图1，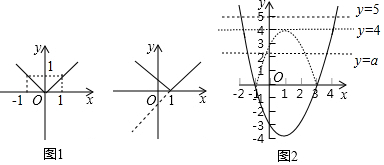

（2）类比探究
作函数y=|x-1|的图象，可以转化为分段函数y=$\left\{\begin{array}{l}{x-1（x≥1）}\\{-x+1（x＜1）}\end{array}\right.$；
（3）拓展提高
把函数y=x²-2x-3的图象在x轴下面部分，沿x轴进行翻折，与x轴上及上面部分组成了函数y=|x²-2x-3|的图象，如图2右图；
（4）实际运用
1）函数y=|x²-2x-3|的图象与x轴有 2个交点，对应方程|x²-2x-3|=0有2个实根；
2）函数y=|x²-2x-3|的图象与直线y=5有 2个交点，对应方程|x²-2x-3|=5有2个实根；
3）函数y=|x²-2x-3|的图象与直线y=4有3个交点，对应方程|x²-2x-3|=4有3个实根；
4）关于x的方程|x²-2x-3|=a有4个实根时，a的取值范围是 0＜a＜4．
故答案为y=$\left\{\begin{array}{l}{x-1（x≥1）}\\{-x+1（x＜1）}\end{array}\right.$；2，2；2，2；3，3；0＜a＜4．

点评 本题考查了几何变换综合题：熟练掌握折叠的性质、一次函数和二次函数的性质；会利用分类讨论的方法解决绝对值函数；会利用数形结合的思想，把求方程的解的个数问题转化为两函数的交点个数问题．