题目内容
7.(1)解不等式组$\left\{\begin{array}{l}{2(2x-1)≤3x+4}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\end{array}\right.$,并把解集在数轴上表示出来.(2)解分式方程:$\frac{3}{{x}^{2}-9}$+$\frac{x}{x-3}$=1.
分析 (1)首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集;
(2)首先两边同时乘以x2-9去分母,然后再整理成一元一次方程,再解即可,注意不要忘记检验.
解答 解:(1)$\left\{\begin{array}{l}{2(2x-1)≤3x+4①}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1②}\end{array}\right.$,
由①得:x≤6,
由②得:x≥-1,
画图:
所以原不等式组的解集为-1≤x≤6;
(2)两边同乘以x2-9,得:
3+x(x+3)=x2-9,
化简,得3x=-12,
解得:x=-4,
经检验,x=-4是原方程的根.
点评 此题主要考查了解一元一次不等式组,以及分式方程,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
17.过⊙O内一点M的最长弦为10cm,最短弦长为8cm,则OM的长为( )
| A. | 9cm | B. | 6cm | C. | 3cm | D. | $\sqrt{41}$cm |
2.若a-2=b+c,则a(a-b-c)+b(b+c-a)-c(a-b-c)的值为( )
| A. | 4 | B. | 2 | C. | 1 | D. | 8 |
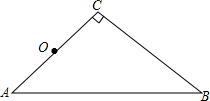 在等腰直角三角形ABC中,∠C=90°,BC=2cm.以AC的中点O为对称中心,画出与△ABC关于点O成中心对称的△DEF,点A、B、C的对称点分别是点D、E、F,并求出BE的长.
在等腰直角三角形ABC中,∠C=90°,BC=2cm.以AC的中点O为对称中心,画出与△ABC关于点O成中心对称的△DEF,点A、B、C的对称点分别是点D、E、F,并求出BE的长.
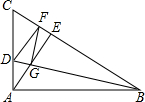 在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.
在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由. 如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.
如图,将平行四边形ABCD折叠,使点A与C重合,折痕为EF.若∠A=60,AD=4,AB=6,则AE为$\frac{19}{4}$.