题目内容
9.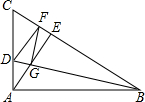 在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.
在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.
分析 ∠AGD=∠FGD,易证△BAD≌△BFD,得到DA=DF,∠ADB=∠FDB,则△DAG≌≌△DFG,所以∠AGD=∠FGD.
解答 解:∠AGD=∠FGD,
理由如下:∵∠BAC=90°,DF⊥BC,
∴∠BAC=∠BFD=90°,
在Rt△BAD和Rt△BFD中
$\left\{\begin{array}{l}{BD=BD}\\{BF=AB}\end{array}\right.$
∴△BAD≌△BFD,
∴DA=DF,∠ADB=∠FDB,
在△DAG和△DFG中
$\left\{\begin{array}{l}{DA=DF}\\{∠ADB=∠FDB}\\{DG=DG}\end{array}\right.$
∴△DAG≌≌△DFG,
∴∠AGD=∠FGD.
点评 本题主要考查了全等三角形的判定与性质,熟悉全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目