题目内容
17. 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,AE平分∠BAD,交BC于E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,AE平分∠BAD,交BC于E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.(1)求证:BE=CF;
(2)在AB上取一点M,使得BM=2DE,连接ME
①求证:ME⊥BC;
②求∠EMC的度数.
分析 (1)由等腰直角三角形的性质可知∠ABC=∠ACB=45°,由FC⊥BC可知∠ACF=45°,从而得出∠ABE=∠ACF;由∠BAE、∠CAF均为∠EAC的余角可得出∠BAE=∠CAF,结合AB=AC即可得出△ABE≌△ACF,根据全等三角形的性质即可得出结论;
(2)①过点E作EQ⊥AB于点Q,由△AEQ≌△AED可得出QE=DE;根据∠BQE=90°和∠QBE=45°可得出∠BEQ=45°、BQ=QE,再由BE=2DE=2QE即可得出∠QEC=45°,由此可得出∠BEM=90°,即ME⊥BC;②设DE=a,则BM=2a,根据等腰直角三角形的性质可用含a的代数式表示AB和BD,由边与边的关系可得出AM=ME,结合MC=MC可证得Rt△MAC≌Rt△MEC,即∠EMC=∠AMC,再根据角与角的关系即可得出结论.
解答 (1)证明:∵△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵FC⊥BC,
∴∠ACF+∠ACB=90°,
∴∠ACF=45°=∠ABE.
∵∠BAC=90°,FA⊥AE,
∴∠BAE+∠EAC=90°=∠CAF+∠EAC,
∴∠BAE=∠CAF.
在△ABE和△ACF中,$\left\{\begin{array}{l}{∠ACF=∠ABE}\\{AB=AC}\\{∠BAE=∠CAF}\end{array}\right.$,
∴△ABE≌△ACF(ASA),
∴BE=CF.
(2)①证明:过点E作EQ⊥AB于点Q,如图所示.
∵AE平分∠BAD,
∴∠QAE=∠DAE,
在△AEQ和△AED中,$\left\{\begin{array}{l}{∠QAE=∠DAE}\\{∠ADE=∠AQE=90°}\\{AE=AE}\end{array}\right.$
∴△AEQ≌△AED(AAS),
∴QE=DE.
∵∠BQE=90°,∠QBE=45°,
∴∠BEQ=45°,
∴BQ=QE,
又∵BM=2DE=QE,
∴QM=QE,
∴∠QEM=∠QME=$\frac{90°}{2}$=45°,
∴∠BEM=∠BEQ+∠QEM=90°,
∴ME⊥BC.
②解:设DE=a,则BM=2a.
∵△BEM为等腰直角三角形,
∴BE=EM=$\frac{\sqrt{2}}{2}$BM=$\sqrt{2}$a,
∴BD=BE+DE=($\sqrt{2}$+1)a.
∵△ABC为等腰直角三角形,AD⊥BC,
∴AB=$\sqrt{2}$BD=$\sqrt{2}$×($\sqrt{2}$+1)a=(2+$\sqrt{2}$)a,
∵BM=2a,
∴AM=(2+$\sqrt{2}$)a-2a=$\sqrt{2}$a,
∴AM=EM.
在Rt△MAC和Rt△MEC中,$\left\{\begin{array}{l}{AM=EM}\\{MC=MC}\end{array}\right.$,
∴Rt△MAC≌Rt△MEC(HL),
∴∠EMC=∠AMC,
又∵∠BME=45°,
∴∠EMC=$\frac{1}{2}$(180°-45°)=67.5°.
点评 本题考查了全等三角形的判定及性质、等腰直角三角形的性质以及角的计算,解题的关键是:(1)证明△AEQ和△AED全等;(2)①得出∠BEM=90°;②通过边角关系找出AM=EM.本题属于中档题,难度不大,但做题过程较繁琐,解决该题型题目时,根据全等三角形的性质找出相等的量是关键.

 阅读快车系列答案
阅读快车系列答案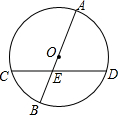 如图,AB为⊙O的直径,CD为弦,AE=7cm,BE=3cm,∠AED=60°,则弦CD的长为( )
如图,AB为⊙O的直径,CD为弦,AE=7cm,BE=3cm,∠AED=60°,则弦CD的长为( )| A. | 2$\sqrt{21}$cm | B. | 4$\sqrt{6}$cm | C. | 2$\sqrt{22}$cm | D. | 8cm |
| 类别 | 彩电 | 冰箱 | 洗衣机 |
| 进价(元/台) | 2000 | 1600 | 1000 |
| 售价(元/台) | 2300 | 1800 | 1100 |
(1)用含x的代数式表示洗衣机的台数.
(2)商场至多可以购买冰箱多少台?
(3)购买冰箱多少台时,能使商场销售完这批家电后获得的利润最大?最大利润为多少元?
 如图,抛物线y1=-x2+4x和直线y2=2x在同一直角坐标系中.当y1>y2时,x的取值范围是0<x<2.
如图,抛物线y1=-x2+4x和直线y2=2x在同一直角坐标系中.当y1>y2时,x的取值范围是0<x<2.