题目内容
8.某射击队从四名队员中选拨一名参赛,选拨赛中,每名队员平均成绩$\overline{x}$与方差S2如表,要选一个平均成绩高且发挥稳定的人参赛,应是( )| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| S2 | 1 | 1 | 1.2 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
分析 先根据平均数的大小找出成绩高的同学,再根据方差的意义找出发挥稳定的学生即可.
解答 解:∵甲的平均数是8,乙的平均数是9,丙的平均数是9,丁的平均数是8,
∴成绩高的是乙和丙,
∵S乙2=1,S丙2=1.2,
∴S乙2<S丙2,
∴乙的平均成绩高且发挥稳定;
故选:B.
点评 本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.也考查了平均数.

练习册系列答案
相关题目
19.下列计算正确的是( )
| A. | (-2a)2=2a2 | B. | a6÷a3=a2 | C. | 3a•a2=3a3 | D. | (-2a2)•(-3a3)=6a6 |
13.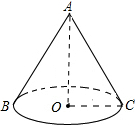 如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
 如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )| A. | 9π | B. | 24π | C. | 15π | D. | 30π |
20.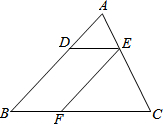 如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=4:7,那么CF:CB等于( )
如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=4:7,那么CF:CB等于( )
 如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=4:7,那么CF:CB等于( )
如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=4:7,那么CF:CB等于( )| A. | 7:11 | B. | 4:8 | C. | 4:7 | D. | 3:7 |
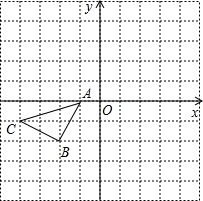 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: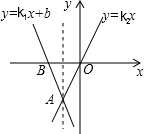 如图,直线y=k1x+b经过点A(-1,-2)和点B(-2,0),直线y=k2x经过点A,则二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,不等式k2x<k1x+b<0的解集为x<-1.
如图,直线y=k1x+b经过点A(-1,-2)和点B(-2,0),直线y=k2x经过点A,则二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,不等式k2x<k1x+b<0的解集为x<-1.