如图.已知圆锥的底面周长为6πcm.高为4cm.则这个圆锥的全面积是( )A．9πB．24πC．15πD．30π 题目和参考答案——青夏教育精英家教网—

题目内容

13．

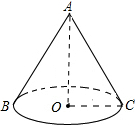如图，已知圆锥的底面周长为6πcm，高为4cm，则这个圆锥的全面积是（　　）

A．

9π

B．

24π

C．

15π

D．

30π

分析先利用圆的周长公式得到底面圆的半径为3，然后根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式求出圆锥的侧面积，再求底面积与侧面积的和即可．

解答解：设圆锥的底面圆的半径为r，
则2πr=6π，
解得r=3，
所以圆锥的母线长=$\sqrt{{3}^{2}+{4}^{2}}$=5（cm），
所以这个圆锥的全面积=π•3²+$\frac{1}{2}$•6π•5=24π（cm²）．
故选B．

点评本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．

练习册系列答案

快乐暑假假期作业云南人民出版社系列答案

相关题目

3．

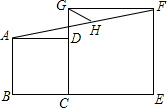如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=2，CE=3，H是AF的点，则GH的长是（　　）

4．计算：$\root{3}{27}$-（$\sqrt{3}$-1）⁰+（$\frac{1}{2}$）^-2-4$\sqrt{2}$sin45°．

1．

已知：如图，点C是AB的中点，AD=CE，CD=BE．求证：CD∥BE．

8．某射击队从四名队员中选拨一名参赛，选拨赛中，每名队员平均成绩$\overline{x}$与方差S²如表，要选一个平均成绩高且发挥稳定的人参赛，应是（　　）

	甲	乙	丙	丁
$\overline{x}$	8	9	9	8
S²	1	1	1.2	1.3

18．（2×10³）²×（3×10^-3）=1.2×10⁴．（结果用科学记数法表示）

5．对于锐角α，sinα的值不可能为（　　）

2．先化简，再求值：$\frac{（x-2）（x+3）}{{{x^2}-9}}•\frac{x-3}{{{x^2}-2x}}$，其中x=-2．

3．

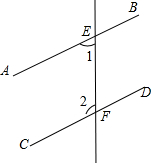如图，直线AB∥CD，直线EF分别交AB，CD于点E，F，若∠1=55°，则∠2的度数为（　　）

试题分类