题目内容
18.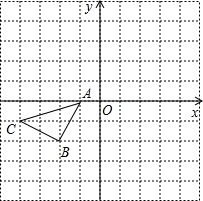 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:(1)分别写出点A与点B的坐标;
(2)作出△ABC关于坐标原点成中心对称的△A1B1C1;
(3)已知点M的坐标为(1,4),请你在x轴上寻找一点P,使得|PM-PB|的值最大,并写出点P的坐标.
分析 (1)直接根据图形写出点A与点B的坐标;
(2)分别作出点A、点B和点C关于原点的对称点A1、B1、C1顺次连接各点即可得到图形;
(3)作M点关于x轴对称点N(1,-4),连接BN,交x轴与点P,此时|PM-PB|的值最大,求出直线NB的解析式,即可求出P点坐标.
解答 解:(1)A(-1,0),B(-2,-2);
(2)作图如图1,
(3)作图如图2,
作M点关于x轴对称点N(1,-4),
连接BN,交x轴与点P,此时|PM-PB|的值最大,
根据点N(1,4),点B(2,2),
则直线NB解析式为y=-$\frac{2}{3}$x-$\frac{10}{3}$,
令y=0,x=-5,
则P(-5,0).
点评 本题主要考查了作图旋转变换的知识,利用轴对称变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键,此题有一定的难度.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
2. 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.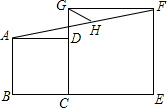 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=3,H是AF的点,则GH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=3,H是AF的点,则GH的长是( )
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=3,H是AF的点,则GH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=3,H是AF的点,则GH的长是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1.5 |
8.某射击队从四名队员中选拨一名参赛,选拨赛中,每名队员平均成绩$\overline{x}$与方差S2如表,要选一个平均成绩高且发挥稳定的人参赛,应是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| S2 | 1 | 1 | 1.2 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,在△ABC中,AB=AC,∠BAC=120°,D、E为BC边上的点,且∠DAE=60°.
如图,在△ABC中,AB=AC,∠BAC=120°,D、E为BC边上的点,且∠DAE=60°.