题目内容
18．
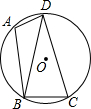如图，已知四边形ABCD内接于圆O，连结BD，∠BAD=105°，∠DBC=75°．求证：BD=CD．
分析 根据圆内接四边形对角互补可得∠DCB+∠BAD=180°，然后可得∠DCB=180°-105°=75°，再根据等角对等边可得BD=CD．
解答 证明：∵四边形ABCD内接于圆O，
∴∠DCB+∠BAD=180°，
∵∠BAD=105°，
∴∠DCB=180°-105°=75°，
∵∠DBC=75°，
∴∠DCB=∠DBC=75°，
∴BD=CD．
点评 此题主要考查了圆内接四边形的性质，关键是掌握圆内接四边形对角互补．
练习册系列答案
相关题目
7．某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩计算了甲成绩的平均数和方差（如图见小宇的作业）
解：${\overline x_甲}$=$\frac{1}{5}$（9+4+7+4+6）=6
s甲2=$\frac{1}{5}$[（9-6）2+（4-6）2+（7-6）2+（4-6）2+（6-6）2]
=$\frac{1}{5}$（9+4+1+4+0）
=3.6
甲、乙两人射箭成绩统计表
（1）求a和乙的方差；
（2）请你从平均数和方差的角度分析谁将被选中．
解：${\overline x_甲}$=$\frac{1}{5}$（9+4+7+4+6）=6
s甲2=$\frac{1}{5}$[（9-6）2+（4-6）2+（7-6）2+（4-6）2+（6-6）2]
=$\frac{1}{5}$（9+4+1+4+0）
=3.6
甲、乙两人射箭成绩统计表
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 9 | 4 | 7 | 4 | 6 |
| 乙成绩 | 7 | 5 | 7 | a | 7 |
（2）请你从平均数和方差的角度分析谁将被选中．