题目内容
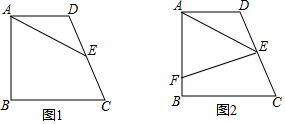
13.已知四边形ABCD中,AB=BC,∠ABC=90°,AD∥BC,E为CD上一点,且AE=AB,∠BAE=60°(1)如图1,①求∠AED的度数;
②求证:DE=CE;
(2)如图2,过E作EF⊥CD交AB于点F,若$\frac{BF}{AF}$=$\frac{1}{2}$,求$\frac{AD}{BC}$的值.
分析 (1)①连接BE,作EH⊥AB于H,根据题意得到△ABE是等边三角形,根据等腰三角形的性质得到∠AEH=30°,∠BEC=∠C=75°,计算即可;
②根据平行线分线段成比例定理证明即可;
(2)作AG⊥AE交EF的延长线于G,证明△AFG≌△ADE,得到AF=AD,根据题意计算即可.
解答 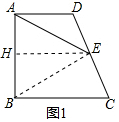 解:(1)①如图1,连接BE,作EH⊥AB于H,
解:(1)①如图1,连接BE,作EH⊥AB于H,
∵AE=AB,∠BAE=60°,
∴△ABE是等边三角形,
∴∠AEB=∠ABE=60°,
∵EH⊥AB,
∴∠AEH=30°,
∵∠ABC=90°,∠ABE=60°,
∴∠EBC=30°,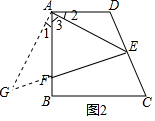
∵BE=BC,
∴∠BEC=∠C=75°,
∴∠AED=180°-75°-60°=45°;
②∵EH⊥AB,∠ABC=90°,AD∥BC,
∴AD∥BC∥EH,又AH=HB,
∴DE=CE;
(2)如图2,作AG⊥AE交EF的延长线于G,
∵EF⊥CD,∠AED=45°,
∴∠AEG=45°,
∴∠AGE=45°,
∴AG=AE,
∵∠GEF=∠BAD=90°,
∴∠1+∠3=∠2+∠3=90°,
∴∠1=∠2,
在△AFG和△ADE中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AG=AE}\\{∠AGE=∠AED}\end{array}\right.$,
∴△AFG≌△ADE,
∴AF=AD,
∵$\frac{BF}{AF}$=$\frac{1}{2}$,
∴$\frac{AF}{AB}$=$\frac{2}{3}$,
∴$\frac{AD}{BC}$=$\frac{2}{3}$.
点评 本题考查的是相似三角形的性质,掌握相似三角形的判定定理和性质定理、等边三角形的判定定理和性质定理、等腰三角形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
(1)设从甲仓库运送到A港口的物资为x吨,用含x的式子填写下表:
(2)求总费用y(元)与x(箱)之间的函数关系式,并写出x的取值范围;
(3)求出最低费用,并说明费用最低时的调配方案.
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | x | 100-x |
| B港 | 80-x | x-30 |
(3)求出最低费用,并说明费用最低时的调配方案.
 已知抛物线y=-x2+4x+5与x轴的交点A,B(A在B的左边),顶点为P.
已知抛物线y=-x2+4x+5与x轴的交点A,B(A在B的左边),顶点为P.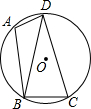 如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.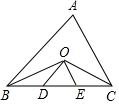 如图,等边△ABC的边长为6cm,BO,CO分别是∠ABC和∠ACB的平分线,且OD∥AB,OE∥AC.求△ODE的周长.
如图,等边△ABC的边长为6cm,BO,CO分别是∠ABC和∠ACB的平分线,且OD∥AB,OE∥AC.求△ODE的周长.