题目内容
19．函数y=$\frac{x-3}{3x+2}$中，自变量x的取值范围是x≠-$\frac{2}{3}$．分析 根据分式有意义的条件是分母不为0；分析原函数式可得关系式3x+2≠0，解可得自变量x的取值范围．
解答 解：根据题意，有3x+2≠0，
解可得x≠-$\frac{2}{3}$；
故自变量x的取值范围是x≠-$\frac{2}{3}$，
故答案为x≠-$\frac{2}{3}$．
点评 本题考查了函数自变量的取值范围问题，函数自变量的范围一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为0；
（3）当函数表达式是二次根式时，被开方数为非负数．
练习册系列答案
相关题目
9．
如图，已知向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$，那么下列结论正确的是（ ）
如图，已知向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$，那么下列结论正确的是（ ）| A． | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B． | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ | C． | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D． | $\overrightarrow a+\overrightarrow c=-\overrightarrow b$ |
10．下列图形中，既是轴对称又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．
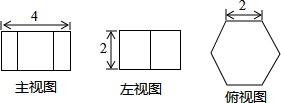如图是某几何体的三视图，则该几何体的表面积为（ ）
如图是某几何体的三视图，则该几何体的表面积为（ ）| A． | 16+6$\sqrt{3}$ | B． | 16+12$\sqrt{3}$ | C． | 24+6$\sqrt{3}$ | D． | 24+12$\sqrt{3}$ |
已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根，k为正整数．
酒驾猛于虎，但很多人不以为是，为了加强人们对酒驾危害的认识，交警部门加大了对酒驾的检查力度．某市交警在2015年2月28日这天对本市各大主要交通路口进行车辆检查，如图，AC是该市解放路的一段，AE，BF，CD都是南北方向的街道，与解放路AC的交叉路口分别是A，B，C．已知出警点D位于点A的北偏东45°方向、点B的北偏东30°方向上，BD=2km，∠DBC=30°．
8．
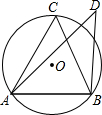如图，若锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），则下列三个结论：①sin∠C＞sin∠D；②cos∠C＞cos∠D；③tan∠C＞tan∠D中，正确的结论为（ ）
如图，若锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），则下列三个结论：①sin∠C＞sin∠D；②cos∠C＞cos∠D；③tan∠C＞tan∠D中，正确的结论为（ ）| A． | ①② | B． | ②③ | C． | ①②③ | D． | ①③ |
9．
阳泉同学参加周末社会实践活动，到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数：
32 39 45 55 60 54 60 28 56 41
51 36 44 46 40 53 37 47 45 46
（1）前10株西红柿秧上小西红柿个数的平均数是47，中位数是49.5，众数是60；
（2）若对这20个数按组距为8进行分组，请补全频数分布表及频数分布直方图
（3）通过频数分布直方图试分析此大棚中西红柿的长势．
阳泉同学参加周末社会实践活动，到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数：32 39 45 55 60 54 60 28 56 41
51 36 44 46 40 53 37 47 45 46
（1）前10株西红柿秧上小西红柿个数的平均数是47，中位数是49.5，众数是60；
（2）若对这20个数按组距为8进行分组，请补全频数分布表及频数分布直方图
| 个数分组 | 28≤x＜36 | 36≤x＜44 | 44≤x＜52 | 52≤x＜60 | 60≤x＜68 |
| 频数 | 2 | 5 | 7 | 4 | 2 |