题目内容
9.解方程:①(公式法)x2-2$\sqrt{2}$x+1=0;
②2x2-7x+6=0.
③(配方法)2x2-4x+1=0.
④x(x-2)=2-x.
分析 ①找出一元二次方程中的二次项系数a,一次项系数b及常数项c,计算出根的判别式大于0,然后将a,b及c的值代入求根公式,即可求出方程的解;
②分解因式,即可得出两个一元一次方程,求出方程的解即可;
③先把方程两边都除以2,使二次项的系数为1,然后再配上一次项系数一半的平方,利用配方法解方程.
④移项,直接提公因式即可.
解答 解:①(公式法)x2-2$\sqrt{2}$x+1=0;
这里a=1,b=-2$\sqrt{2}$,c=1,
∵b2-4ac=8-4=4>0,
∴x=$\frac{2\sqrt{2}±\sqrt{4}}{2×1}$=$\sqrt{2}$±1,
则x1=$\sqrt{2}$+1,x2=$\sqrt{2}$-1;
②2x2-7x+6=0.
(2x-3)(x-2)=0,
2x-3=0,x-2=0,
∴x1=$\frac{3}{2}$,x2=2;
③(配方法)2x2-4x+1=0.
x2-2x=-$\frac{1}{2}$,
x2-2x+1=-$\frac{1}{2}$+1,
(x-1)2=$\frac{1}{2}$,
x-1=±$\frac{\sqrt{2}}{2}$,
∴x1=1+$\frac{\sqrt{2}}{2}$,x2=1-$\frac{\sqrt{2}}{2}$;
④x(x-2)=2-x.
x(x-2)+(x-2)=0,
(x-2)(x+1)=0,
∴x-2=0,x+1=0,
∴x1=2,x2=-1.
点评 本题考查了解一元二次方程的应用,解此题的关键是熟练掌握解一元二次方程的方法.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
19.若有理数满足$\frac{1}{a}+\frac{1}{b}$=0,则下列说法不正确的是( )
| A. | a与b的差是正数 | B. | a与b的和为0 | C. | a与b的积为负数 | D. | a与b的商为-1 |
18.近似数0.60的准确值a的取值范围是( )
| A. | 0.555≤a<0.655 | B. | 0.55≤a≤0.65 | C. | 0.595<a≤0.605 | D. | 0.595≤a<0.605 |
 如图,在△ABC中,∠BAC=90°,AB=AC,BD是中线,AF⊥BD,F为垂足,过点C作AB的平行线交AF的延长线于点E.求证:(1)∠1=∠2;(2)AB=2CE.
如图,在△ABC中,∠BAC=90°,AB=AC,BD是中线,AF⊥BD,F为垂足,过点C作AB的平行线交AF的延长线于点E.求证:(1)∠1=∠2;(2)AB=2CE. 我市某服装厂主要做外贸服装,由于技术改良,2012年全年每月的产量y(单位:万件)与月份x之间可以用如图所示的一次函数表示,但由于“欧债危机”的影响,销售受困,为了不使货积压,老板只能是降低利润销售,原来每件可赚10元,从1月开始每月每件降低0.5元.试求:
我市某服装厂主要做外贸服装,由于技术改良,2012年全年每月的产量y(单位:万件)与月份x之间可以用如图所示的一次函数表示,但由于“欧债危机”的影响,销售受困,为了不使货积压,老板只能是降低利润销售,原来每件可赚10元,从1月开始每月每件降低0.5元.试求: (1)作△ABC的外接圆(尺规作图,保留作图痕迹,不写作法);
(1)作△ABC的外接圆(尺规作图,保留作图痕迹,不写作法); 如图,AC=BG,AB,CG垂直平分线交于点F,求证:∠ABF=∠CGF.
如图,AC=BG,AB,CG垂直平分线交于点F,求证:∠ABF=∠CGF.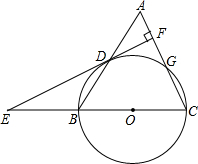 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.