题目内容
14. 如图,AC=BG,AB,CG垂直平分线交于点F,求证:∠ABF=∠CGF.
如图,AC=BG,AB,CG垂直平分线交于点F,求证:∠ABF=∠CGF.
分析 连接AF,CF,根据线段垂直平分线的性质得到AE=BF,CF=GF,推出△AFC≌△BFG,得到∠AFC=∠BFG,于是得到∠AFB=∠CFG,证得△AFB∽△CFG,即可得到结论.
解答 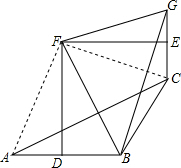 解:连接AF,CF,
解:连接AF,CF,
∵AB,CG垂直平分线交于点F,
∴AE=BF,CF=GF,
在△AFC与△BFG中,$\left\{\begin{array}{l}{AF=BF}\\{CF=FG}\\{AC=BG}\end{array}\right.$,
∴△AFC≌△BFG,
∴∠AFC=∠BFG,
∴∠AFB=∠CFG,
∵$\frac{AF}{BF}=\frac{CF}{GF}=1$,
∴△AFB∽△CFG,
∴∠ABF=∠CGF.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5.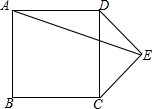 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )
 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )| A. | $\frac{1}{2}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{10}}{5}$ |
2.正比例函数y=6x的图象与反比例函数y=$\frac{4}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第一、三象限 |
 已知△ABC的内接矩形EFGH的两个顶点E、F在BC边上,另外两个顶点H、G分别在AB、AC边上.
已知△ABC的内接矩形EFGH的两个顶点E、F在BC边上,另外两个顶点H、G分别在AB、AC边上.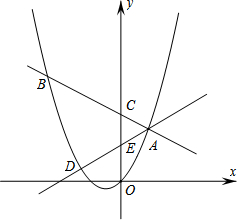 如图,抛物线y=x2+bx+c过原点O及点A(1,2),过点A的直线交抛物线于另一点B,交y轴于点C,过点A的另一条直线交抛物线于另一点D,交y轴于点E,且∠ACE=∠AEC.
如图,抛物线y=x2+bx+c过原点O及点A(1,2),过点A的直线交抛物线于另一点B,交y轴于点C,过点A的另一条直线交抛物线于另一点D,交y轴于点E,且∠ACE=∠AEC.