Question

1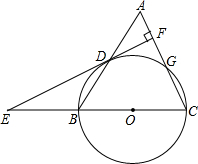．如图，等腰三角形ABC中，AC=BC=10，AB=12，以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．
（1）求证：直线EF是⊙O的切线；
（2）求DF、CG的长．

Answer 1

分析 （1）连接OD，根据直角所对的圆周角是直角和等腰三角形的性质证明OD⊥EF即可；
（2）连接CD、BG，根据勾股定理求出CD的长，计算出△ABC的面积，根据面积公式进行计算即可．

解答 （1）证明：连接OD，
∵OB=OD，∴∠OBD=∠ODB，
∵AC=BC，∴∠CBA=∠A，
∴∠ODB=∠A，
∴OD∥AC，又DF⊥AC，
∴OD⊥EF，
∴直线EF是⊙O的切线；
（2）连接CD、BG，
∵BC为⊙O的直径，
∴∠CDB=∠CGB=90°，
∵AC=BC，∴BD=$\frac{1}{2}$AB=6，
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=8，
∴△ABC的面积为$\frac{1}{2}$×12×8=48，
∴△ADC的面积为24，即$\frac{1}{2}$×10×DF=24，
DF=4.8；
$\frac{1}{2}$×10×BG=48，BG=9.6，
CG=$\sqrt{B{C}^{2}-B{G}^{2}}$=2.8．

点评 本题考查的是切线的判定、圆周角定理，掌握直角所对的圆周角是直角、经过半径的外端垂直于半径的性质是圆的切线是解题的关键．