题目内容
20. 如图,在△ABC中,∠BAC=90°,AB=AC,BD是中线,AF⊥BD,F为垂足,过点C作AB的平行线交AF的延长线于点E.求证:(1)∠1=∠2;(2)AB=2CE.
如图,在△ABC中,∠BAC=90°,AB=AC,BD是中线,AF⊥BD,F为垂足,过点C作AB的平行线交AF的延长线于点E.求证:(1)∠1=∠2;(2)AB=2CE.
分析 (1)易证∠CAE=∠ABD,即可证明△ACE≌△BAD,可得∠1=∠2;
(2)根据△ACE≌△BAD可得CE=AD.
解答 证明:(1)∵∠CAE+∠BAE=90°,∠BAE+∠ABD=90°,
∴∠CAE=∠ABD,
在△ACE和△BAD中,
$\left\{\begin{array}{l}{∠CAE=∠ABD}\\{AB=AC}\\{∠BAD=∠ACE=90°}\end{array}\right.$,
∴△ACE≌△BAD,(ASA)
∴∠1=∠2;
(2)∵△ACE≌△BAD,
∴CE=AD,
∵BD是AC边上的中线,
∴CE=$\frac{1}{2}AC=\frac{1}{2}AB$,
∴AB=2CE.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACE≌△BAD是解题的关键.

练习册系列答案
相关题目
11.2008年元月某一天的天气预报中,北京的最低温度是-12℃,哈尔滨的最低温度是-26℃,这一天北京的最低气温比哈尔滨的最低气温高( )
| A. | 14℃ | B. | -14℃ | C. | 38℃ | D. | -38℃ |
15.从某市8000名初三学生中,随机地抽取300名学生,测得他们所穿鞋的鞋号(单位:厘米)由小到大排列得到一个样本,则这个样本数据的平均数、中位数、众数和方差四个指标中,鞋厂最感兴趣的指标是( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
5.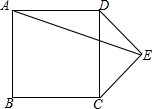 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )
 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=( )| A. | $\frac{1}{2}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{10}}{5}$ |



