题目内容
14. 如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是20.
如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是20.
分析 由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,AC=12,
∴OA=$\frac{1}{2}$AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴BD=2OB=20.
故答案为:20.
点评 此题考查了平行四边形的性质以及勾股定理.注意掌握平行四边形的对角线互相平分.

练习册系列答案
相关题目
4.下列二次根式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{24}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{18}$ |
2. 把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )
把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )
 把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )
把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
9.要判断命题“若a>b,则a2>b2”是假命题,可举得反例是( )
| A. | a=1,b=-2 | B. | a=1,b=0 | C. | a=2,b=1 | D. | a=2,b=-1 |
6.对于函数y=-2x+1有以下四个结论,其中正确的结论是( )
| A. | 函数图象必经过点(-2,1) | B. | 函数图象经过第一、二、三象限 | ||
| C. | 函数值y随x的增大而增大 | D. | 当x>$\frac{1}{2}$,时,y<0 |
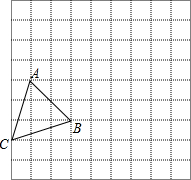 如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.
如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.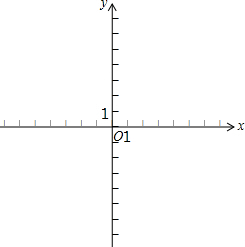 在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).