题目内容
6. 在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
分析 (1)设此一次函数的表达式为y=kx+b(k≠0).由点A、B的坐标利用待定系数法即可求出该函数的表达式;
(2)设点P的坐标为(a,-a+5).根据三角形的面积公式即可列出关于a的含绝对值符号的一元一次方程,解方程即可得出结论.
解答 解:(1)设此一次函数的表达式为y=kx+b(k≠0).
∵一次函数的图象经过点A(2,3)与点B(0,5),
∴$\left\{\begin{array}{l}2k+b=3\\ b=5.\end{array}\right.$,解得$\left\{\begin{array}{l}k=-1\\ b=5.\end{array}\right.$.
∴此一次函数的表达式为y=-x+5.
(2)设点P的坐标为(a,-a+5). ∵B(0,5),
∵B(0,5),
∴OB=5.
∵S△POB=10,
∴$\frac{1}{2}×5×|a|=10$.
∴|a|=4.
∴a=±4.
∴点P的坐标为(4,1)或(-4,9).
点评 本题考查了待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)利用待定系数法求出函数表达式;(2)找出关于a的含绝对值符号的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
相关题目
16.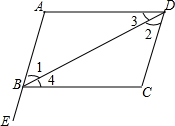 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠C=∠CBE | D. | ∠C+∠ABC=180° |
11.下列事件为必然事件的是( )
| A. | 小王参加本次数学考试,成绩是500分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
18.下列命题是假命题的是( )
| A. | 平行四边形的对角相等 | B. | 四条边都相等的四边形是菱形 | ||
| C. | 正方形的两条对角线互相垂直 | D. | 矩形的两条对角线互相垂直 |
18.下列说法中,正确的是( )
| A. | 在同一平面内,不相交的两条直线必平行 | |
| B. | 过任意一点可作一条已知直线的平行线 | |
| C. | 两条直线被第三条直线所截,所得到同位角相等 | |
| D. | 两条直线的交点叫做垂足 |
 如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.
如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1. 如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是20.
如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是20.