题目内容
19.方程x2-4x=0的解为x1=0,x2=4.方程(x-3)(x+1)=x-3的解是x1=3,x2=0.分析 方程x2-4x=0根据提公因式法可以解答本题;方程(x-3)(x+1)=x-3,先移项,再提公因式法即可解答本题.
解答 解:∵x2-4x=0,
∴x(x-4)=0,
解得,x1=0,x2=4;
∵(x-3)(x+1)=x-3,
∴(x-3)(x+1)-(x-3)=0,
∴(x-3)(x+1-1)=0,
∴(x-3)x=0,
解得,x1=3,x2=0,
故答案为:x1=0,x2=4;x1=3,x2=0.
点评 本题考查解一元二次方程-因式分解法,解答此类问题的关键是根据方程的特点,选择合适的方法解答方程.

练习册系列答案
相关题目
15.从一个多边形的一个顶点出发,至多可引5条对角线,则该多边形的内角和为( )
| A. | 1620° | B. | 1440° | C. | 1260° | D. | 1080° |
9. 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (-1,-1) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
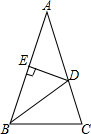 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E. 如图,在△ABC中,AB=9,BC=3,BD平分∠ABC,且AD⊥BD于点D,点E为AC中点,连接DE,则DE的长为3.
如图,在△ABC中,AB=9,BC=3,BD平分∠ABC,且AD⊥BD于点D,点E为AC中点,连接DE,则DE的长为3. (1)有理数a,b在数轴上位置如图所示,求-|a|+|b|;
(1)有理数a,b在数轴上位置如图所示,求-|a|+|b|;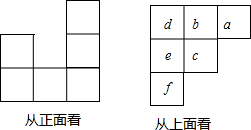 用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:
用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题: