题目内容
10.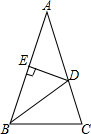 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.(1)写出图中一对全等角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明;
(3)求AD:AC的值.
分析 (1)利用等腰三角形的性质和三角形的内角和可求出图中所有角的度数,从而可得到△ADE≌△BDE,△ABC∽△BCD;
(2)利用有两组角对应相等的两个三角形相似可证明△ABC∽△BCD;
(3)先证明AD=BD=BC,再利用△ABC∽△BCD得到$\frac{AC}{BC}$=$\frac{BC}{CD}$,则AC•(AC-AD)=AD2,然后解关于AC的一元二次方程即可得到AD:AC的值.
解答 解:(1)△ADE≌△BDE,△ABC∽△BCD;
(2)∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-36°)=72°,
∵BD为角平分线,
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC=36°,
∴∠CBD=∠A,
而∠BCD=∠ACB,
∴△ABC∽△BCD;
(3)∵∠A=∠ABD=36°,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∵△ABC∽△BCD,
∴$\frac{AC}{BC}$=$\frac{BC}{CD}$,
即AC•(AC-AD)=AD2,
整理得AD2+AC•AD-AC2=0,
解得AD=$\frac{-1+\sqrt{5}}{2}$AC或AD=$\frac{-1-\sqrt{5}}{2}$AC(舍去),
∴AD:AC的值为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了相似三角形的性质和等腰三角形的性质.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
6.下列有理数-(-2),(-1)6,-|-5|,-3.14,-0,其中负数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
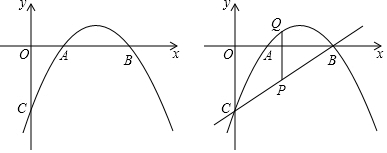





 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面上升1米时,水面的宽度为2$\sqrt{2}$米.
如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面上升1米时,水面的宽度为2$\sqrt{2}$米.