题目内容
20.计算:$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$.分析 根据绝对值的定义分情况解答,即可确定代数式的值,从而求解即可.
解答 解:当a>0,b>0,c>0,d>0,e>0,f>0,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$=9;
当a<0,b>0,c>0,d>0,e>0,f>0,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$=7;
当a<0,b<0,c>0,d>0,e>0,f>0,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$=5;
当a<0,b<0,c<0,d>0,e>0,f>0,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$=3;
当a<0,b<0,c<0,d<0,e>0,f>0,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$=1;
当a<0,b<0,c<0,d<0,e<0,f>0,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$=-1;
当a<0,b<0,c<0,d<0,e<0,f<0,$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|d|}{d}$+$\frac{|e|}{e}$+$\frac{|f|}{f}$+$\frac{|ab|}{ab}$+$\frac{|cd|}{cd}$+$\frac{|ef|}{ef}$=-3.
点评 此题考查绝对值问题,根据任何数的绝对值一定是非负数,正确确定字母的值,是解决本题的关键.

| 质量m(千克) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 售价s(元) | 2 | 2.3 | 2.6 | 2.9 | 3.2 | 3.5 |
| 刹车时的车速x(km/h) | 0 | 10 | 20 | 40 | 60 |
| 刹车距离y(m) | 0 | 0.3 | 1.0 | 3.6 | 7.8 |
(2)若该型号的汽车正在行驶时,发现前方约31m处有一只羊横穿公路,驾驶员紧急刹车,在距羊1m处停下,此时车速为多少?是正常行驶还是超速行驶?
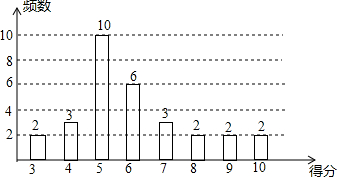 为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )
为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )| A. | m=n=$\overline x$ | B. | m=n<$\overline x$ | C. | m<n<$\overline x$ | D. | n<m<$\overline x$ |
| A. | sinα<cosα<tanα | B. | sinα<tanα<cosα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
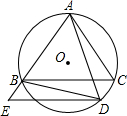 ⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.
⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.