题目内容
1.若0<α<30°,则sinα,cosα,tanα的大小关系是( )| A. | sinα<cosα<tanα | B. | sinα<tanα<cosα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
分析 首先根据0<α<30°,可得0<sinα<$\frac{1}{2}$,0<tanα<$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{2}$<cosα<1,据此判断出sinα<cosα,tanα<cosα;然后判断出sinα<tanα,即可判断出sinα,cosα,tanα的大小关系.
解答 解:∵0<α<30°,
∴0<sinα<$\frac{1}{2}$,0<tanα<$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{2}$<cosα<1,
∴sinα<cosα,tanα<cosα,
又∵$\frac{\sqrt{3}}{2}$<cosα<1,
∴tanα=$\frac{sinα}{cosα}>sina$,
∴sinα<tanα<cosα.
故选:B.
点评 此题主要考查了锐角三角函数的增减性,要熟练掌握,解答此题的关键是要明确:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).

练习册系列答案
相关题目
16.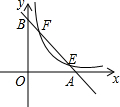 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
13.关于x的两个多项式乘积:(x+a)(x+b)的结果是( )
| A. | x2-ab | B. | x2+ab | C. | x2+(a-b)x+ab | D. | x2+(a+b)x+ab |
10.下列命题中的假命题是( )
| A. | 当a=b时,有a2=b2 | |
| B. | 经过已知直线外一点,有且只有一条直线与已知直线平行 | |
| C. | 互为相反数的两个数的和为0 | |
| D. | 相等的角是对顶角 |
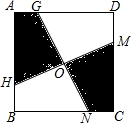 如图,点O是边长为2的正方形ABCD的对称中心,过点O作OM⊥ON,分别交正方形边于M、N、G、H,则当OM、ON绕点O旋转时,图中的阴影部分是否关于O点为中心对称?这两部分的面积是否改变?请说明理由.
如图,点O是边长为2的正方形ABCD的对称中心,过点O作OM⊥ON,分别交正方形边于M、N、G、H,则当OM、ON绕点O旋转时,图中的阴影部分是否关于O点为中心对称?这两部分的面积是否改变?请说明理由.