题目内容
15.化简:$\frac{x-3}{x^2+6x+9}+\frac{x}{9-x^2}$,并求出当x=2时原式的值.分析 把分式的分子与分母分解因式后进行约分,再根据分式的加法法则进行加法运算,最后化成最简分式即可.
解答 解:$\frac{x-3}{x^2+6x+9}+\frac{x}{9-x^2}$
=$\frac{x-3}{(3+x)^{2}}+\frac{x}{(3-x)(3+x)}$
=$\frac{(x-3)(3-x)}{(3+x)^{2}(3-x)}+\frac{x(3+x)}{(3+x)^{2}(3-x)}$
=$\frac{9(x-1)}{(3+x)^{2}(3-x)}$,
把x=2代入$\frac{9(x-1)}{(3+x)^{2}(3-x)}=\frac{9}{25}$.
点评 本题主要考查对分式的基本性质,约分、通分,最简分式,最简公分母,分式的加减、乘除运算,分式的化简求值等知识点的理解和掌握,能熟练地进行有关分式的运算是解此题的关键.

练习册系列答案
相关题目
16.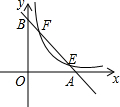 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
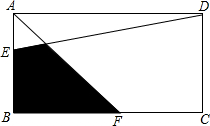 面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积.
面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积.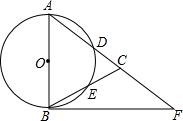 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在A的延长线上,且∠A=2∠CBF.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在A的延长线上,且∠A=2∠CBF.