题目内容
7.把下列各式分解因式:(1)3ax-3ay+xy-y2
(2)4xy+1-4x2-y2
(3)a4b+a3b2-a2b3-ab4
(4)x6-y6-2x3+1
(5)x2(x+1)-y(xy+x)
(6)x3+3x-4.
分析 (1)先分组,再提公因式,最后分解即可;
(2)先分组,再根据公式分解因式,最后分解即可;
(3)先分组,再提公因式,最后分解即可;
(4)先分组,再根据公式分解因式,最后分解即可;
(5)去括号后分组,再提公因式,最后分解即可;
(6)先分组,再分解因式,最后分解即可.
解答 解:(1)3ax-3ay+xy-y2
=3a(x-y)+y(x-y)
=(x-y)(3a+y);
(2)4xy+1-4x2-y2
=1-(4x2-4xy+y2)
=1-(2x-y)2
=(1+2x-y)(1-2x+y);
(3)a4b+a3b2-a2b3-ab4
=a3b(a+b)-ab3(a+b)
=(a+b)(a3b-ab3)
=(a+b)ab(a2-b2)
=ab(a+b)(a+b)(a-b)
=ab(a+b)2(a-b);
(4)x6-y6-2x3+1,
=(x6-2x3+1)-yy6
=(x3-1)2-(y3)2
=(x3-1+y3)(x3-1-y3);
(5)x2(x+1)-y(xy+x)
=x3+x2-xy2-xy
=(x3-xy2)+(x2-xy)
=x(x+y)(x-y)+x(x-y)
=x(x-y)(x+y+1);
(6)x3+3x-4
=(x3-1)+3x-3
=(x-1)(x2+x+1)+3(x-1)
=(x-1)(x2+x+1+3)
=(x+1)(x2+x+4).
点评 本题考查了分解因式,能正确分组是解此题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
15.二元一次方程x+3y=7的正整数解的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
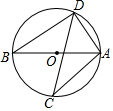 如图,AB为⊙O的直径,CD是⊙O的弦,∠ACD=25°,则∠BAD=65°.
如图,AB为⊙O的直径,CD是⊙O的弦,∠ACD=25°,则∠BAD=65°.