题目内容
17.已知y=y1+y2,y1与x成正比例,y2与x2成反比例,且当x=2时,y=0,当x=-1时,y=$\frac{9}{2}$,求y与x之间的函数关系式.分析 根据正比例与反比例的定义设出函数表达式,将两组x、y的对应值代入,然后解二元一次方程组即可.
解答 解:∵y1与x成正比例,y2与x成反比例,
∴设y1=k1x,y2=$\frac{{k}_{2}}{{x}^{2}}$,
∴y=k1x+$\frac{{k}_{2}}{{x}^{2}}$,
∴$\left\{\begin{array}{l}{2{k}_{1}+\frac{{k}_{2}}{4}=0}\\{-{k}_{1}+{k}_{2}=\frac{9}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-\frac{1}{4}}\\{{k}_{2}=2}\end{array}\right.$,
∴y与x之间的函数关系式为y=-$\frac{1}{4}$x+$\frac{2}{{x}^{2}}$.
点评 本题考查了函数关系式,利用了待定系数法求函数解析式,先设出两个正比例函数解析式是解题关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
2.“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具,某自行车专卖店的自行车销售量自2014年底起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该自行车专卖店前4个月的自行车销量的月平均增长率相同,则该自行车专卖店4月份卖出125辆自行车.
(2)若该自行车专卖店,A型车的进价为500元/辆,B型车进价为1000元/辆.下表是近两周的销售情况:
①A型号的自行车的销售单价为700元,B型号的自行车的销售单价为1300元;
②考虑到自行车需求不断增加,该自相车专卖店准备用不超过25万的金额再进购一批两种规格的自行车共300辆,求B型号最多能够多少辆;
③在②在的条件下,售完这300辆自行车能否实现利润为8.5万元的目标?若能,请给出采购方案,若不能,请说明理由.
(1)若该自行车专卖店前4个月的自行车销量的月平均增长率相同,则该自行车专卖店4月份卖出125辆自行车.
(2)若该自行车专卖店,A型车的进价为500元/辆,B型车进价为1000元/辆.下表是近两周的销售情况:
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 12辆 | 8辆 | 18800元 |
| 第二周 | 20辆 | 10辆 | 27000元 |
②考虑到自行车需求不断增加,该自相车专卖店准备用不超过25万的金额再进购一批两种规格的自行车共300辆,求B型号最多能够多少辆;
③在②在的条件下,售完这300辆自行车能否实现利润为8.5万元的目标?若能,请给出采购方案,若不能,请说明理由.
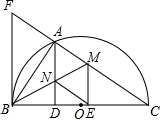 如图,以BC为直径,以O为圆心的半圆交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,BC2=CF•AC,cos∠ABD=$\frac{3}{5}$,AD=12.
如图,以BC为直径,以O为圆心的半圆交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,BC2=CF•AC,cos∠ABD=$\frac{3}{5}$,AD=12.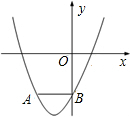 如图,已知二次函数y=x2+bx+c(c≠0)的图象经过点A(-2,m)(m<0),与y轴交于点B,AB∥x轴,且AB=OB.
如图,已知二次函数y=x2+bx+c(c≠0)的图象经过点A(-2,m)(m<0),与y轴交于点B,AB∥x轴,且AB=OB.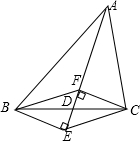 如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.
如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.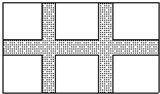 如图,在宽为20m,长为32m的矩形耕地上,修筑宽度一样的三条道路(如图),把耕地分成大小相等的六块作为实验田,要使实验田面积为504m2,求每条道路的宽度为多少米?
如图,在宽为20m,长为32m的矩形耕地上,修筑宽度一样的三条道路(如图),把耕地分成大小相等的六块作为实验田,要使实验田面积为504m2,求每条道路的宽度为多少米?