题目内容
9.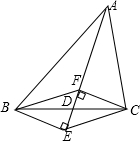 如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.
如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.
分析 利用全等三角形的判定方法得出△CFD≌△BED(AAS),进而利用一组对边平行且相等的四边形是平行四边形得出即可.
解答 解:四边形BECF是平行四边形.
理由:∵AD是△ABC的中线,
∴DC=BD,
在△CFD和△BED中
∵$\left\{\begin{array}{l}{∠CFD=∠BED}\\{∠CDF=∠BDE}\\{DC=BD}\end{array}\right.$,
∴△CFD≌△BED(AAS),
∴BE=FC,
∵CF⊥AD,BE⊥AD,
∴CF∥EB,
∴四边形BECF是平行四边形(一组对边平行且相等的四边形是平行四边形).
故答案为:平行四边形,一组对边平行且相等的四边形是平行四边形.
点评 此题主要考查了平行四边形的判定以及全等三角形的判定与性质,得出△CFD≌△BED是解题关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
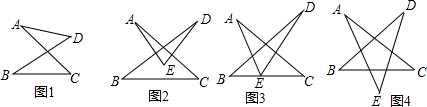
4.观察如图的图形,找规律,填表答题.

(1)把表补充完整,并回答其中哪个是自变量,哪个是因变量?
(2)图形的边数a是小梯形个数n的函数吗?

| 小梯形个数n | 1 | 2 | 3 | 4 | … | n |
| 图形的边数a | 4 | 7 | 10 | 13 | … | 3n+1 |
(2)图形的边数a是小梯形个数n的函数吗?
 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)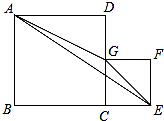 如图,正方形ABCD和正方形CEFG的边长分别为a,$\frac{a}{2}$.
如图,正方形ABCD和正方形CEFG的边长分别为a,$\frac{a}{2}$. 数a,b在数轴上的位置如图所示,化简:|a+b|-|a-b|+|a|-|b|.
数a,b在数轴上的位置如图所示,化简:|a+b|-|a-b|+|a|-|b|.