题目内容
4.某超市在一楼至二楼间安装了一自动扶梯,以均匀的速度向上行驶,张明与高丽同时从自动扶梯上走到二楼(扶梯本身也在行驶),如果张明与高丽都在均速运动,且张明每分钟走动的级数是高丽的2倍,已知张明走了27级到达扶梯顶部,而高丽走了18级到达顶部(设张明、高丽每次只跨一级台阶),则扶梯露在外面的部分有54级.分析 如果设女孩上梯速度为x级/分,自动扶梯的速度为y级/分,扶梯露在外面的部分有S级.题中有两个等量关系,男孩走27级的时间等于扶梯走(S-27)级的时间;女孩走18级的时间等于扶梯走(S-18)级的时间,据此列出方程组,求出S的值即可.
解答 解:设女孩上梯速度为x级/分,自动扶梯的速度为y级/分,扶梯露在外面的部分有S级,则男孩上梯的速度为2x级/分.
由题意,有$\left\{\begin{array}{l}{\frac{27}{2x}=\frac{S+27}{y}}\\{\frac{18}{x}=\frac{S-18}{y}}\end{array}\right.$,
解得S=54.
答:扶梯露在外面的部分有54级.
故答案为:54.
点评 本题考查应用类问题,分式方程在行程问题中的应用,分析题意,找到合适的等量关系是解决问题的关键.本题属于竞赛题型,有一定难度.难点在于自动扶梯在上升,具有一定的速度,同时甲、乙也在上楼梯,变化量较多.解题时要善于抓住不变量,只有不变量才是列方程的依据.另外,本题求解时设的未知数x、y,只设不求,这种方法在解复杂的应用题时常用来帮助分析数量关系,便于解题.

练习册系列答案
相关题目
14.某人下午6点到7点之间外出购物,出发和回来时发现表上的时针和分针的夹角都为110°,此人外出购物共用了( )分钟.
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
18.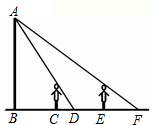 如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
 如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )| A. | 8米 | B. | 6米 | C. | 4.5米 | D. | 3米 |
14. 如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
 如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2014 | B. | ($\frac{1}{2}$)2014 | C. | ($\frac{\sqrt{2}}{2}$)2015 | D. | ($\frac{1}{2}$)2015 |
 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片,如图,一个油桶由两个圆形铁片和一个长方形铁片相配套,生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套? 如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.
如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.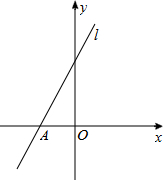 如右图,在直角坐标系中,点A(-4,0),直线l与x轴夹角为60°,点B在直线l上,且AB=10,求点B的坐标.
如右图,在直角坐标系中,点A(-4,0),直线l与x轴夹角为60°,点B在直线l上,且AB=10,求点B的坐标. 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图: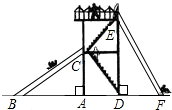 如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.
如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.