题目内容
18.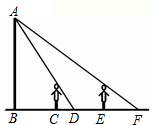 如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )| A. | 8米 | B. | 6米 | C. | 4.5米 | D. | 3米 |
分析 根据已知得出∠E=∠EAB=45°,得出AB=BE,再进而利用△DCM∽△DBA,得出$\frac{DC}{MC}$=$\frac{BD}{AB}$,进而求出即可.
解答 解:∵当她继续往前走到D处时,测得此时影子DE的长刚好是自己的身高,
∴DF=DE=1.5m,
∴∠E=∠EAB=45°,
∴AB=BE,
∵MC∥AB,
∴△DCM∽△DBA,
∴$\frac{DC}{MC}$=$\frac{BD}{AB}$,
设AB=x,则BD=x-1.5=x-1.5,
∴$\frac{1}{1.5}$=$\frac{x-1.5}{x}$,
解得:x=4.5.
∴路灯A的高度AB为4.5m.
故选C.
点评 此题主要考查了相似三角形的判定与性质、等腰直角三角形的判定和性质等知识,解题的关键是寻找相似三角形,学会用方程的思想思考问题,根据已知得出AB=BE是本题的突破点.

练习册系列答案
相关题目
8.观察下列等式:
①1=12;②2+3+4=32;③3+4+5+6+7=52;④4+5+6+7+8+9+10=72;…请你根据观察得到的规律判断下列各式正确的是( )
①1=12;②2+3+4=32;③3+4+5+6+7=52;④4+5+6+7+8+9+10=72;…请你根据观察得到的规律判断下列各式正确的是( )
| A. | 1006+1007+1008+…+3019=20132 | B. | 1006+1007+1008+…+3020=20132 | ||
| C. | 1007+1008+1009+…+3019=20132 | D. | 1008+1009+1010+…+3020=20132 |
9.下列四个数中最小的数是( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | 5 |

