题目内容
13.如图,抛物线y=-$\frac{1}{2}$x2+bx+c的图象与x轴交于A(-4,0)、B(1,0)两点,与y轴交于点C,连结AC.(1)求该抛物线的函数表达式;
(2)动点M从点A出发,沿AC方向以$\sqrt{5}$个单位/秒的速度向终点C匀速运动,动点N从点O出发,沿着OA方向以$\frac{3}{2}$个单位/秒的速度向终点A匀速运动,设点M、N同时出发,运动时间为t(0<t≤2);
①连结MN、NC,当t为何值时,△CMN为直角三角形;
②在两个动点运动的过程中,该抛物线上是否存在点P,使得以点O、P、M、N为顶点的四边形是平行四边形?若存在,求出点P的坐;若不存在,请说明理由.

分析 (1)由题意假设抛物线的解析式为y=-$\frac{1}{2}$(x+4)(x-1),展开化简即可;
(2)①分两种情形①当∠MNC=90°,如图1中,作MH⊥AB于H,当∠NMC=90°时,作MH⊥OA于H,分别构建方程即可解决问题;
②分三种情形分别讨论由题意M((2t-4,t),N(-$\frac{3}{2}$t,0),设P(m,n).a、当MN为对角线时,由中点坐标公式可知$\frac{m+0}{2}$=$\frac{2t-4-\frac{3}{2}t}{2}$,$\frac{n+0}{2}$=$\frac{t+0}{2}$,解得m=$\frac{1}{2}$t-4,n=t,可得P($\frac{1}{2}$t-4,t),把点P坐标代入y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2,解方程即可解决.b、当OM为对角线时,同法可得P($\frac{7}{2}$t-4,t).c、ON为对角线时,不存在;
解答 解:(1)由题意假设抛物线的解析式为y=-$\frac{1}{2}$(x+4)(x-1),
即y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2.
(2)显然∠NCM≠90°.
①当∠MNC=90°,如图1中,作MH⊥AB于H.
∵MH∥OC,
∴$\frac{AM}{AC}$=$\frac{AH}{AO}$=$\frac{MH}{OC}$,
∵AM=$\sqrt{5}$t,PA=4.OC=2,AC=2$\sqrt{5}$,
∴HM=t.AH=2t,HN=4-$\frac{3}{2}$t-2t=4-$\frac{7}{2}$t,
由△MNH∽△CNO,可得$\frac{HN}{CO}$=$\frac{MH}{NO}$,
∴$\frac{4-\frac{7}{2}t}{2}$=$\frac{t}{\frac{3}{2}t}$,
解得t=$\frac{16}{21}$,
当∠NMC=90°时,作MH⊥OA于H,如图2中,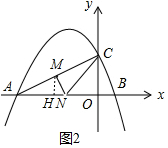
由△AHM∽△MHN,可得HM2=AH•HN,
∴t2=2t•(4-$\frac{7}{2}$t),
解得t=1,
综上所述,t=$\frac{16}{21}$s或1s时,△CNM是直角三角形.
②由题意M((2t-4,t),N(-$\frac{3}{2}$t,0),设P(m,n).
a、当MN为对角线时,由中点坐标公式可知$\frac{m+0}{2}$=$\frac{2t-4-\frac{3}{2}t}{2}$,$\frac{n+0}{2}$=$\frac{t+0}{2}$,
解得m=$\frac{1}{2}$t-4,n=t,
∴P($\frac{1}{2}$t-4,t),把点P坐标代入y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2,
∴t=-$\frac{1}{2}$×$\frac{1}{2}$t×($\frac{1}{2}$t-5),
解得t=2或0(舍弃),
此时P(-3,2).
b、当OM为对角线时,同法可得P($\frac{7}{2}$t-4,t),
把点P坐标代入y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2,得到t=-$\frac{1}{2}$×$\frac{7}{2}$t×($\frac{7}{2}$t-5)
解得t=$\frac{62}{49}$.
此时P($\frac{3}{7}$,$\frac{62}{49}$).
c、ON为对角线时,不存在.
综上所述,满足条件的点P坐标P(-3,2)或($\frac{3}{7}$,$\frac{62}{49}$).
点评 本题考查二次函数综合题、直角三角形的判定和性质、中点坐标公式、待定系数法、平行四边形的判定和性质等知识,解题的关键是灵活应用中点坐标公式解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | (0,0) | B. | (-6,0) | C. | (0,-4) | D. | (-1,0) |
 如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )
如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )| A. | 点O1 | B. | 点O2 | C. | 点O3 | D. | 点O4 |
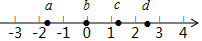 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |
 如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4).
如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4). 如图,点E、F分别在菱形ABCD的边AD、CD上,△EFD为等边三角形,G是BE的中点,延长AG交BC于点H,已知AB=6,四边形GHCF的面积是△ABG的面积的2倍,则ED的长为9-3$\sqrt{5}$.
如图,点E、F分别在菱形ABCD的边AD、CD上,△EFD为等边三角形,G是BE的中点,延长AG交BC于点H,已知AB=6,四边形GHCF的面积是△ABG的面积的2倍,则ED的长为9-3$\sqrt{5}$.
 如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.
如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B. 如图,在△ABC中,AD⊥BC于D,AB=4,AC=3,DC=$\frac{9}{5}$.
如图,在△ABC中,AD⊥BC于D,AB=4,AC=3,DC=$\frac{9}{5}$.