题目内容
3. 如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4).
如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4).(1)求a的值;
(2)作Rt△OAB,使∠BOA=90°,且OB=2OA,求点A坐标;
(3)在(2)的条件下,过点A作直线AC⊥x轴于点C,交抛物线y=ax2(a≠0)于点D,将该抛物线向左或向右平移t(t>0)个单位长度,记平移后点D的对应点为D′,点B的对应点为B′.当CD′+OB′的值最小时,请直接写出t的值和平移后相应的抛物线解析式.
分析 (1)将点B(-2,4)代入y=ax2(a≠0)求解即可;
(2)当点A作第一象限时,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N.先证明△BNO∽△OMA,依据相似三角形的性质可求得OM和AM的长,从而可得到点A的坐标;大概点A在第三象限内时,过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N.同理可得到OM=1,MA=2,从而可得到点A的坐标;
(3)当点A在第三象限时,点B与点D重合,不成立;当点A在第一象限时,过点B作BE⊥x轴,垂足为E,作点O关于y=4的对称点O′,连结EO′交x轴与点B′,由平移的性质可得到EB′=CD′,然后依据轴对称的性质可知OB′=O′B′,则当点O′、B′、E在一条直线上时CD′+OB′的值最小,从而可求得B′F=BB′=1,然后依据二次函数的平移规律可求得到平移后抛物线的解析式.
解答 解:(1)将点B(-2,4)代入y=ax2(a≠0)得4a=4,解得:a=1.
(2)如图①,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N.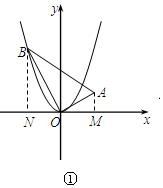
∴∠OMA=∠BNO=90°,
∴∠NBO+∠NOB=90°.
∵∠BOA=90°,
∴∠NOB+∠MOA=90°,
∴∠NBO=∠MOA,
∴△BNO∽△OMA,
∴$\frac{BN}{OM}=\frac{NO}{MA}=\frac{BO}{OA}=\frac{2}{1}$.
∵BN=4,NO=2,
∴OM=2,MA=1.
∴A点坐标为(2,1).
如图②,过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N.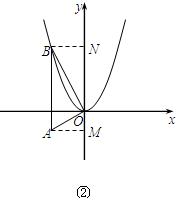
同上可得OM=1,MA=2.
∴A点坐标为(-2,-1).
综上所述,A点坐标为(2,1)或(-2,-1).
(3)当点A在第三象限时,点B与点D重合,不成立.
如图③所示:过点B作BE⊥x轴,垂足为E,作点O关于y=4的对称点O′,连结EO′交x轴与点B′.
由平移的性质可知BB′=DD′=t,EB′=CD′.
∴OB′+CD′=OB′+B′E.
∵点O与点O′关于y=4对称,
∴O′(0,8),O′B′=OB′.
∴OB′+CD′=OB′+B′E=O′B′+B′E.
由两点之间线段最短可知当点B平移到点B′处时CD′+OB′的值最小.
∵F为OO′的中点,B′F∥OE,
∴B′F=$\frac{1}{2}$OE=1.
∴BB′=1.
∴t=1.
∴平移后抛物线的解析式为y=(x-1)2,即y=x2-2x+1.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、相似三角形的性质和判定、平移的性质、轴对称最短路径问题,找出CD′+OB′取的最小值的条件是解题的关键.

| A. | 3.14 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{\frac{4}{9}}$ |
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨所需运费(元/吨) | 120 | 160 | 100 |
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应如何安排车辆?并求出最少总运费.
| 过点C作CE⊥CB于点C,与MN交于点E ∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°, ∴∠BCD=∠ACE. ∵四边形ACDB内角和为360°, ∴∠BDC+∠CAB=180°. ∵∠EAC+∠CAB=180°, ∴BD+AB=$\sqrt{2}$CB. | ∴∠EAC=∠BDC 又∵AC=DC, ∴△ACE≌△DCB, ∴AE=DB,CE=CB, ∴△ECB为等腰直角三角形, ∴BE=$\sqrt{2}$CB. 又∵BE=AE+AB, ∴BE=BD+AB. |
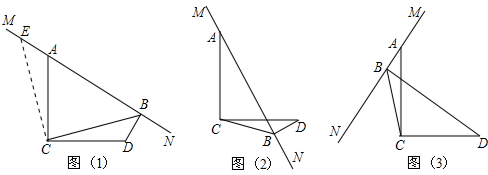
(1)当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明.
(2)MN在绕点A旋转过程中,当∠BCD=30°,BD=$\sqrt{2}$时,则CD=2,CB=$\sqrt{3}$+1.
 如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )
如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )