题目内容
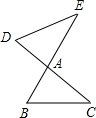如图，线段BE、CD相交于点A，连接DE、BC，请添加一个条件，使△ADE与△ABC相似，且点B的对应点为点D，这个条件可以是考点：相似三角形的判定
专题：
分析：由图形可知△ADE和△ABC中已知有一组对顶角相等，所以可以加∠B=∠D，或∠E=∠C，或
=
都可．
| AD |
| AB |
| AE |
| AC |
解答：解：∵∠DAE=∠BAC，且点B的对应点为点D，
根据三角形相似的判定方法，可以有两组角对应相等或一组角相等，且这组角的两边对应成比例都可证明两三角形相似，
∴可加∠B=∠D或∠E=∠C，或
=
，
故答案为：∠B=∠D（或∠E=∠C，或
=
）．
根据三角形相似的判定方法，可以有两组角对应相等或一组角相等，且这组角的两边对应成比例都可证明两三角形相似，
∴可加∠B=∠D或∠E=∠C，或
| AD |
| AB |
| AE |
| AC |
故答案为：∠B=∠D（或∠E=∠C，或
| AD |
| AB |
| AE |
| AC |
点评：本题主要考查相似三角形的判定方法，掌握三角形相似的判定方法是解题的关键，注意对应点．
练习册系列答案
阅读快车系列答案
相关题目
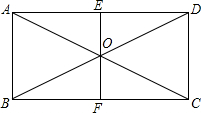如图，点O为矩形ABCD对角线的交点，过点O作EF⊥BC于点F，若AB=2cm，BC=4cm，求四边形AECF的面积．
燕子风筝的骨架如图所示，它是以直线L为对称轴的轴对称图形．已知∠1=∠4=45°，求∠2和∠5的度数．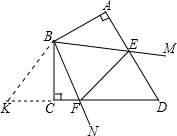
已知四边形ABCD中，AB⊥AD，BC⊥CD，AB=BC，∠ABC=120°，∠MBN=
如图，将矩形ABCD折叠，使点D与B重合，点C落在点C′外，折痕为EF，如果∠ABE=20°，则∠EFC′=