题目内容
现有5元、2元、1元纸币共有30张（每种都有），面值共100元，试求5元、2元、1元纸币各多少张？
考点：二元一次方程的应用
专题：
分析：设1元纸币有x张，2元纸币有y张，则5元纸币有30-x-y张，根据面值共100元列方程式即可解题．
解答：解：设1元纸币有x张，2元纸币有y张，则5元纸币有30-x-y张，
则x+2y+5×（30-x-y）=100，
整理得：150-4x-3y=100，
那么x=
，
∵x是正数，
∴50-3y只能是4的倍数的正整数，
那么y=2，6，10，14时，对应的x为11，8，5，2，
答：1元纸币有11张，2元纸币有2张，5元纸币有17张，或1元纸币有8张，2元纸币有6张，5元纸币有16张，或1元纸币有5张，2元纸币有10张，5元纸币有15张，或1元纸币有2张，2元纸币有14张，5元纸币有14张．
则x+2y+5×（30-x-y）=100，
整理得：150-4x-3y=100，
那么x=
| 50-3y |
| 4 |
∵x是正数，
∴50-3y只能是4的倍数的正整数，
那么y=2，6，10，14时，对应的x为11，8，5，2，
答：1元纸币有11张，2元纸币有2张，5元纸币有17张，或1元纸币有8张，2元纸币有6张，5元纸币有16张，或1元纸币有5张，2元纸币有10张，5元纸币有15张，或1元纸币有2张，2元纸币有14张，5元纸币有14张．
点评：本题属于不定方程的灵活应用，关键是用不定方程式表示出未知量之间的关系式．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
如图，在△ABC中，∠BAC的平分线交BC于点D，AB：AC=m：n（m＜n），CD-BD=a，求BC的长．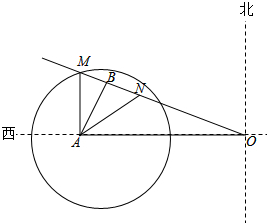
如图，学校A位于工地O的正西方向240米，拖拉机从O出发，沿大路以5米每秒的速度沿北偏西60°方向行使，拖拉机的噪声影响半径为130米，那么大路上行驶的拖拉机的噪声会影响学校吗？如果有影响会有多长时间？用同一种正多边形地砖不能镶嵌成平整的地面的是（ ）
| A、正三角形地砖 |
| B、正方形地砖 |
| C、正五边形地砖 |
| D、正六边形地砖 |
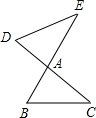如图，线段BE、CD相交于点A，连接DE、BC，请添加一个条件，使△ADE与△ABC相似，且点B的对应点为点D，这个条件可以是将下列各组数据作为三角形的边长，能够组成直角三角形的是（ ）
| A、4，5，6 | ||
| B、1.5，2，2.5 | ||
| C、2，3，4 | ||
D、1，
|