题目内容
 如图,将矩形ABCD折叠,使点D与B重合,点C落在点C′外,折痕为EF,如果∠ABE=20°,则∠EFC′=
如图,将矩形ABCD折叠,使点D与B重合,点C落在点C′外,折痕为EF,如果∠ABE=20°,则∠EFC′=考点:平行线的性质,翻折变换(折叠问题)
专题:计算题
分析:先利用平角的定义计算出∠DEB=160°,再根据折叠的性质得∠DEF=∠BEF,∠EFC′=∠EFC,则∠BEF=
∠DEB=80°,∠AEF=∠AEB+∠BEF=100°,然后利用平行线得性质得到∠EFC=100°,所以∠EFC′=100°.
| 1 |
| 2 |
解答:解:∵∠ABE=20°,
∴∠DEB=180°-20°=160°,
∵矩形ABCD折叠,使点D与B重合,点C落在点C′外,折痕为EF,
∴∠DEF=∠BEF,∠EFC′=∠EFC,
∴∠BEF=
∠DEB=80°,
∴∠AEF=∠AEB+∠BEF=100°,
∵AD∥BC,
∴∠EFC=∠AEF=100°,
∴∠EFC′=100°.
故答案为100.
∴∠DEB=180°-20°=160°,
∵矩形ABCD折叠,使点D与B重合,点C落在点C′外,折痕为EF,
∴∠DEF=∠BEF,∠EFC′=∠EFC,
∴∠BEF=
| 1 |
| 2 |
∴∠AEF=∠AEB+∠BEF=100°,
∵AD∥BC,
∴∠EFC=∠AEF=100°,
∴∠EFC′=100°.
故答案为100.
点评:本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质.

练习册系列答案
相关题目
下列说法错误的是( )
| A、相反数是它本身的数是0 |
| B、绝对值是它本身的数是正数 |
| C、0的绝对值是它本身 |
| D、有理数的相反数仍是有理数 |
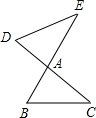 如图,线段BE、CD相交于点A,连接DE、BC,请添加一个条件,使△ADE与△ABC相似,且点B的对应点为点D,这个条件可以是
如图,线段BE、CD相交于点A,连接DE、BC,请添加一个条件,使△ADE与△ABC相似,且点B的对应点为点D,这个条件可以是 如图,在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE,求证:AE=BE+GE.
如图,在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE,求证:AE=BE+GE. 如图,点E是?ABCD中的边BC上的一点,AE交BD于点F,BE=3,BC=4,S△FBE=18,求?ABCD的面积.
如图,点E是?ABCD中的边BC上的一点,AE交BD于点F,BE=3,BC=4,S△FBE=18,求?ABCD的面积.